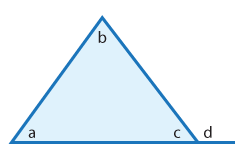
You have already practiced solving problems involving angle measures on the interior of triangles. Now I would like to introduce you to exterior angles. Exterior angles exist on the outside of a vertex of a triangle, but they do not account for the entire area outside of a vertex. To identify an exterior angle, first, extend the sides of a triangle beyond each vertex. The exterior angles are the angles that would form supplementary pairs with each interior angle. The order in which you extend the sides of your triangles does not matter, but for the sake of consistency, you should extend them in the same order within each triangle – clockwise or counter clockwise.

Notice again that when an interior angle and its corresponding exterior angle are combined, they form a linear pair, and their angles would add up to equal one hundred eighty degrees. This fact is true regardless of the orientation you draw your exterior angles.

An additional theorem that was developed as a result of exterior angles is known as the Remote Interior Angles Theorem. Before we discuss this theorem, let me first describe what remote interior angles are. They are the angles not adjacent, or next to, the indicated exterior angles. For example, if I label an exterior angle with a number one above, I’ll label its remote interior angles with the numbers 2 and 3. Because of the three exterior angles, there are three groups of exterior and remote interior angles. The Remote Interior Angles Theorem states that the sum of the remote interior angles is equal to the indicated exterior angle. Take a look at this image and study it for a few moments by pausing this video. When you resume playback, I will further demonstrate the Remote Interior Angles Theorem.

First, let’s observe that we have a dynamic triangle in place – this means I can move any vertex around on the screen. By selecting the check boxes on the screen I can turn on the side extensions, as well as any group of exterior and remote interior angles. Remember the sum of two remote interior angles shown in orange is equal to the indicated exterior angle shown in blue. I will now move parts of this diagram on the screen. Pay close attention to the equation that displays on the screen with each group, and ask yourself if this supports what the theorem states? You may have noticed that sometimes the sums were not entirely accurate. The reason for this is due to the rounding of decimal points by the program used to illustrate the theorem – not because the angles sum incorrectly.

Feel free to download and explore this Geogebra file so that you can form a better understanding of the Remote Interior Angles Theorem. Good luck!