Read the steps on each of these slides, which together build logical proof of the AA similarity property.
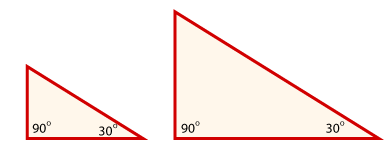
Step 1
The first step is to use a protractor to draw two triangles with two pairs of equal angles. For example, the two triangles above have two pairs of corresponding congruent angles, one pair that measures 90° and the other than measures 30°. Step 2
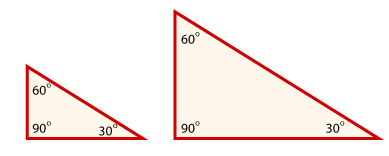
The second step is to measure the third angle of each triangle. What do you think you will find? Click on the Show Me Button below to check your understanding.
The two congruent angles force the third corresponding set of angles to be congruent. Each angle measures 60°.
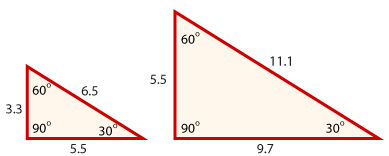
Step 3
The third step is to measure the side lengths and verify that the corresponding sides can be written in the same ratio. In this case \(\mathsf{ \frac {3.3} {5.5} }\) = \(\mathsf{ \frac {5.5} {9.7} }\) = \(\mathsf{ \frac {6.4} {11} }\) = \(\mathsf{ \frac {0.6} {1} }\) Step 4
The last step is to draw a conclusion about these two triangles and then write that conclusion in set of statements. As long as two sets of corresponding angles are congruent, the third set of corresponding angles are also congruent. This also leads to the corresponding sides being in the same ratio. The two triangles are similar by AA. |