In the video below, the instructor will review all the concepts you have learned in this lesson. As you watch the video, pay close attention to what makes a relation or an equation a function.
You may want to use the study guide to follow along. If so, click the button below to download the study guide.
Relations take an input value and transform or compute an output value. There are four ways to represent relations in Algebra: ordered pairs, mapping diagrams, tables of values, and graphs. Two examples of relations are shown here. First the relation of time to the height of bird flying overhead. The second shows the average high temperature per month in a city in Ohio. You may notice, that these relations show that inputs are related to outputs, but they don’t show us how the relationships are made, we’ll talk more about that a little later.
When working with relations, we often focus on the inputs and outputs as separate sets of values. These values are known as the domain and range of a relation. The domain is often referred to as the set of x-coordinates of the ordered pairs, or inputs, while the range is referred to as the set of y-coordinates of the ordered pairs, or outputs. Could you identify the domain and range of the following relations? Pause the video to try them on your own, and resume playback in a moment to check your work. (pause) The domain, or set of x-coordinates in example three is; zero, four, eight, twelve, and sixteen. Whereas the range, or set of y-coordinates is; fifty-nine, seventy-six, eighty-nine, ninety-seven, and one hundred. Notice we list the values from least to greatest. In example four, the domain is: negative six, negative three, two, and five. Whereas the range is: negative one, zero, two, and four. Notice we only listed distinct values, no duplicates. In example four, you may have noticed that two elements of the domain produced multiple elements within the range. These pairings are not permitted in special relations known as functions. A function is a special relation in which each element of the domain corresponds with exactly one element of the range. Therefore we would say that example four is a graph that represents a relation, but does not represent a function. Example three on the other hand does represent a function since each element of the domain corresponds with exactly one element of the range.
Let’s spend some time working with the equations that produce coordinate pairs. Let y squared equal x, and also let x, our input value, equal twenty-five. Then when solving for y, our output value, we would take the square root of both sides of the equation. You should notice that there are two answers to this problem. Both five squared and negative five squared equal twenty-five. Therefore one element of the domain, twenty-five, maps to two elements of the range, negative five and positive five. This is indicative of a relation. Now, take a look at example six on your own. Substitute the provided x-value and solve for y. Pause the video now and resume playback in a moment to check your work (pause). In this case the y-value will be both two and negative two for the x-value provided.
Now we’ll look at examples of functions. These equations represent functions since every element of the domain of the function will produce exactly one element of the range. It is worth noting too that that the domain of each of these functions is all real numbers. Any real number can be used in place of x, and we will be able to determine exactly one y-value for the given x. Please substitute two for x in example seven (silent) in doing so, we establish that y must be thirty seven (silent). In example eight, we substitute negative five for x (silent) and establish that y must be four.
For our final example, you’ll see the problem is written a little differently. This is called function notation, and the letter with a value in parentheses is used only when working with functions. It allows us to name functions and provide input values simultaneously. This example represents the cost, c, of buying tickets, t, to attend a concert. We are being asked to evaluate c at the number four. In other words, what is the cost when buying four tickets? We will substitute as with any relation or function and simplify (silent). It is very important to note that the c-parentheses-four notation does not imply multiplication of c times four. Rather, it is our instruction to evaluate the cost function at a t-value of four.
More often we see function notation written like this (silent) which is read “f of x”. The final example of this video repeats example seven, but using function notation instead. (silent). Thanks for watching, and good luck.
Question
| Input | Output |
|---|---|
| -2 | 9 |
| 0 | 12 |
| 3 | 5 |
| 7 | -3 |
| 10 | 4 |
| 10 | 6 |
| 15 | -5 |
Create a graph and mapping diagram
from the table of values.What is the domain and range?
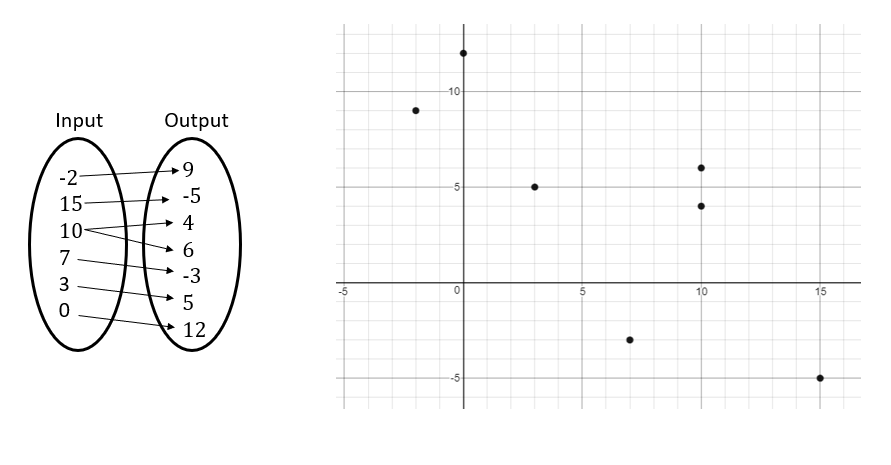
Domain: {-2, 0, 3, 7, 10, 15}
Range: {-5, -3, 4, 5, 6, 9, 12}
