Before you take a scored quiz for this lesson, try this set of practice questions. Your score on this self-check will be similar to that of your scored quiz. If you do not score well on this self-check, please review this lesson and try again.
Which statement is true about the parabola in this graph?
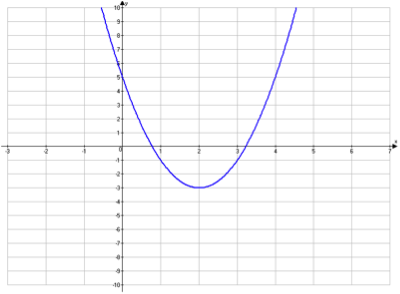
- The parabola opens down.
- The parabola opens left.
- The parabola opens up.
- The parabola opens right.
The parabola opens up.
The parabola opens up.
The parabola opens up.
The parabola opens up.
Define the transformation of the parent function from the graph below.
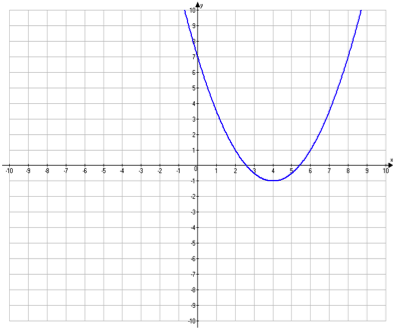
- The parent function f(x) = x2 was shifted down 4 units and to the right 1 unit.
- The parent function f(x) = x2 was shifted down 1 unit and to the right 4 units.
- The parent function f(x) = x2 was shifted up 4 units and to the left 4 units.
- The parent function f(x) = x2 was shifted up 1 unit and to the left 1 unit.
The parent function f(x) = x2 was shifted down 1 unit and to the right 4 units.
The parent function f(x) = x2 was shifted down 1 unit and to the right 4 units.
The parent function f(x) = x2 was shifted down 1 unit and to the right 4 units.
The parent function f(x) = x2 was shifted down 1 unit and to the right 4 units.
What kind of transformations is described by the function
h(x) = (x - 1)2 + 1
if the parent function was f(x) = x2.
- 2 units to the left, 1 unit up
- 1 unit to the right, 1 unit up
- units down, 1 unit to the right
- 1 unit down, 2 units to the left
Subtracting 1 from x moves the function to the right 1 unit, adding 1 moves the function up 1 unit.
Subtracting 1 from x moves the function to the right 1 unit, adding 1 moves the function up 1 unit.
Subtracting 1 from x moves the function to the right 1 unit, adding 1 moves the function up 1 unit.
Subtracting 1 from x moves the function to the right 1 unit, adding 1 moves the function up 1 unit.
Which is the equation for the transformed function below?
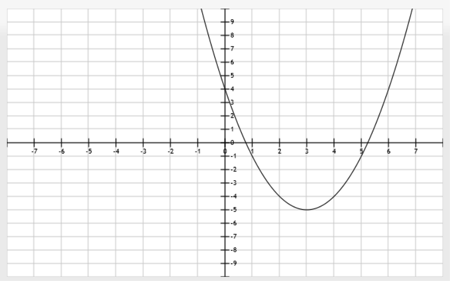
- f(x) = (x + 5)2 + 3.
- f(x) = (x - 3)2 - 5.
- f(x) = (x - 5)2 + 3.
- f(x) = (x + 3)2 - 5.
From the parent function, f(x) = x2, the graph has shifted 3 units to the right (h) and 5 units down (k).
So the equation would be f(x) = (x - 3)2 - 5.
From the parent function, f(x) = x2, the graph has shifted 3 units to the right (h) and 5 units down (k).
So the equation would be f(x) = (x - 3)2 - 5.
From the parent function, f(x) = x2, the graph has shifted 3 units to the right (h) and 5 units down (k).
So the equation would be f(x) = (x - 3)2 - 5.
From the parent function, f(x) = x2, the graph has shifted 3 units to the right (h) and 5 units down (k).
So the equation would be f(x) = (x - 3)2 - 5.
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
The Parent Function
The parent function of a quadratic is defined as ƒ(x) = x2. This is the quadratic function before it is transformed, or changed in any way. The following is the graph of the quadratic parent function.

Vertex Form of a Quadratic
The vertex form of the quadratic function allows us to easily see transformations, or changes, to a quadratic function. The following is the vertex form of a quadratic function.
ƒ(x) = a(x - h)2 + k
The vertex of the quadratic is located at (h, k). The coefficient a tells us whether or not the function will face up or down and how much skinner or fatter it will be than the parent function.
Let's break this form up into its parts as they pertain to transformations.
Reflection
The first transformation is called a reflection. You can tell whether a quadratic function has been reflected by looking at the a coefficient. Concentrate on the following part of the vertex form.
ƒ(x) = ax2

|
If a is positive, the parabola will open up. The equation of the parabola is \(\small\mathsf{ f(x) = x^{2} }\). |
 |
If a is negative, the parabola will open down. The equation for the parabola is \(\small\mathsf{ f(x) = -x^{2} }\). |
Stretch and Compress
The coefficient a also tells you how fat or skinny the function will be or how stretched or compressed the graph will be.
When comparing these transformations to the parent function there are two options.
 |
If |a| > 1, then the function is vertically stretched, and it is narrower than the parent function. The wider graph is the parent function ƒ(x) = x2, and the narrower graph represents the vertically stretched graph ƒ(x) = 2x2. |

|
If |a| < 1, then the function is vertically compressed, and it is wider than the parent function. The narrow graph is the parent function ƒ(x) = x2, and the wider graph represents the vertically compressed graph ƒ(x) = \(\small\mathsf{ \frac{1}{2} }\)x2. |
Horizontal Translation
Now let's concentrate on the next transformation, the horizontal translation. Look at the following portion of the vertex form of the quadratic equation.
ƒ(x) = (x - h)2
Since the h represents the x value in the vertex of a parabola, changing the h value moves the function to the left or right.
 |
When h is positive, the graph moves h units to the right. The graph of ƒ(x) = (x - 4)2 has a horizontal translation of 4 units to the right of the parent function. |
 |
When h is negative, the graph moves h units to the left. The graph of ƒ(x) = (x + 4)2 or ƒ(x) = (x - (-4))2 has a horizontal translation of 4 units to the left of the parent function. |
Vertical Translation
A vertical translation moves the graph of the parabola up or down. Concentrate on the following portion of the vertex form of the quadratic equation.
ƒ(x) = x2 + k
Since the k represents the y value of the vertex, the k value tells you how many units the graph moves up or down.

|
If the k value is positive, the graph moves k units to up. The graph of ƒ(x) = x2 + 4 has a vertical translation of 4 units up from the parent function. |
 |
If the k value is negative, the graph moves k units down. The graph of ƒ(x) = x2 has a vertical translation of 4 units down from the parent function. |
Putting It All Together
Let's put all these transformations together into one graph.
ƒ(x) = -2(x + 1)2 − 5
|
Begin by graphing the parent function.
Next graph the function ƒ(x) = -x2, which is a reflection of the parent function.
Next graph the function ƒ(x) = -2x2, which is a vertical stretch of the function.
Next graph the function ƒ(x) = -2(x + 1)2, which is a horizontal shift of 1 unit to the left.
Finally graph the function ƒ(x) = -2(x + 1)2 - 5, which is a vertical shift of 5 units down.
|






