Archimedes' Principle can be summarized as the relationship between the buoyant force and the weight of the displaced fluid. This can be applied to many situations, including trying to find the density of an unknown object. It can be represented by several different equations. It is important to recognize when to use each one.
Archimedes' Principle
The buoyant force of an object submerged is equal to the weight of the liquid it displaces.
\(\large\mathsf{ F_{buoyant} = \rho V_f g }\)
...where ρ is the density of the fluid, Vf is the volume of the displaced fluid, and g is the acceleration of gravity.
\(\large\mathsf{ F_{buoyant} = m_f g = W_f }\)
...where mg is the mass of the displaced fluid and g is the acceleration of gravity. Wf is the weight of the displaced fluid.
\(\large\mathsf{ F_{buoyant} = F_g - F_{aw} }\)
...where Fg is the weight of the object and Faw is the apparent weight of the object.
That's a lot to take in, so it is best to just work through a few examples and then try some on your own. Use these practice problems to see how these are used in problem solving.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
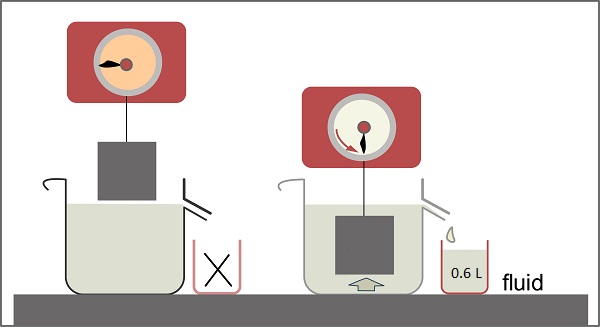
| A 4.68 kg piece of iron displaces 0.600 L of water when submerged. What is the buoyant force on the iron? What is the iron's density? (1 L = 0.001 m3) |
|
\(\mathsf{ \rho_{water} = 997 \text{ kg/m}^3 }\) \(\mathsf{ g = 9.81 \text{ m/s}^2 }\) \(\mathsf{ V_f = 0.600 \text{ L} \cdot 0.001 \text{ m}^3 \text{/L} = 6.00 \times 10^{-4} \text{ m}^3 }\) \(\mathsf{ P = ? \text{ N/m}^2 }\) |
\(\mathsf{ F_{buoyant} = \rho V_f g }\) \(\mathsf{ \rho_{iron} = \frac{m}{V} }\) |
\(\mathsf{ F_{buoyant} = 997 \text{ kg/m}^3 \cdot 6.00 \times 10^{-4} \text{ m}^3 \cdot 9.81 \text{ m/s}^2 }\) \(\mathsf{ F_{buoyant} = 5.86 \text{ N} }\) Use the volume of the displaced fluid as the volume of the object: \(\mathsf{ \rho_{iron} = \frac{4.68 \text{ kg}}{6.00 \times 10^{-4} \text{ m}^3} }\) \(\mathsf{ \rho_{iron} = 7.80 \times 10^4 \text{ N/m}^3 }\) |
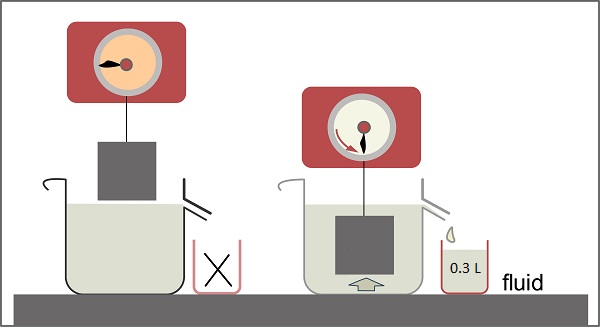
| A 5.89 kg object displaced 0.300 L of water when submerged. What is the buoyant force on the object? What is the object's density? (1 L = 0.001 m3) |
|
\(\mathsf{ \rho_{water} = 997 \text{ kg/m}^3 }\) \(\mathsf{ g = 9.81 \text{ m/s}^2 }\) \(\mathsf{ V_f = 0.300 \text{ L} \cdot 0.001 \text{ m}^3 \text{/L} = 3.00 \times 10^{-4} \text{ m}^3 }\) \(\mathsf{ P = ? \text{ N/m}^2 }\) |
\(\mathsf{ F_{buoyant} = \rho V_f g }\) \(\mathsf{ \rho_{iron} = \frac{m}{V} }\) |
\(\mathsf{ F_{buoyant} = 997 \text{ kg/m}^3 \cdot 3.00 \times 10^{-4} \text{ m}^3 \cdot 9.81 \text{ m/s}^2 }\) \(\mathsf{ F_{buoyant} = 2.93 \text{ N} }\) Use the volume of the displaced fluid as the volume of the object: \(\mathsf{ \rho_{iron} = \frac{5.89 \text{ kg}}{3.00 \times 10^{-4} \text{ m}^3} }\) \(\mathsf{ \rho_{iron} = 1.96 \times 10^4 \text{ N/m}^3 }\) |
| If Alphonso can lift a 113 N object in water with a force of 98 N, what is the magnitude of the buoyant force aiding Alphonso? |
|
\(\mathsf{ F_g = 113 \text{ N} }\) \(\mathsf{ F_{aw} = 98 \text{ N} }\) \(\mathsf{ W_{B} = ? \text{ N} }\) |
\(\mathsf{ F_{buoyant} = F_g - F_{aw} }\) | \(\mathsf{ F_{buoyant} = 113 \text{ N} - 98 \text{ N} }\) \(\mathsf{ F_{buoyant} = 15 \text{ N} }\) |
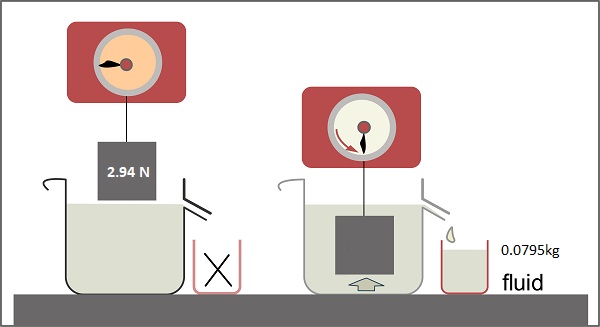
| A piece of brass weighs 2.94 N in air. When the brass is placed beneath the surface of water, it displaces 0.0795 kg of water. What is the apparent weight of the piece of brass as it hangs in the water? |
|
\(\mathsf{ g = 9.81 \text{ m/s}^2 }\) \(\mathsf{ F_g = 2.94 \text{ N} }\) \(\mathsf{ m_g = 0.0795 \text{ kg} }\) \(\mathsf{ F_{aw} = ? \text{ N} }\) |
\(\mathsf{ F_{buoyant} = m_f g }\) \(\mathsf{ F_{buoyant} = F_g - F_{aw} }\) |
\(\mathsf{ F_{buoyant} = 0.0795 \text{ kg} \cdot 9.81 \text{ m/s}^2}\) \(\mathsf{ F_{buoyant} = 0.780 \text{ N}}\) \(\mathsf{ 0.780 = 2.94 - F_{aw} }\) \(\mathsf{ F_{aw} = 2.94 - 0.780 }\) \(\mathsf{ F_{aw} = 2.16 \text{ N} }\) |