Before you take a scored quiz for this lesson, try this set of practice questions. How well you score on this self-check will be similar to your scored quiz. If you do not score well on this self-check, please review this lesson and try again.
Write (2)(2)(2)(2) in exponential form.
- 16
- 24
- 42
Incorrect. The base is 2 and the exponent is the number of times the base is multiplied, which is 4.
Correct.
Incorrect. You mixed up the base and the exponent. The base is 2 and the exponent is the number of times the base is multiplied, which is 4.
Simplify and write the answer in exponential form.
35 · 32 = ?
- 97
- 310
- 37
- 33
Incorrect. Remember, to only add the exponents and keep the base the same. So, the answer would be 3(5 + 2).
Incorrect. It looks like you multiplied the exponents. Remember, to only add the exponents and keep the base the same. So, the answer would be 3(5 + 2).
Correct.
Incorrect. It looks like you subtracted the exponents. Remember, to only add the exponents and keep the base the same. So, the answer would be 3(5 + 2).
Which of the following statements is true?
- -52 = -25 and (-5)2 = 25
- -52 = -25 = (-5)2
- -52 = 25 = (-5)2
Correct. -52 = (-1)(5)(5) = -25 and (-5)2 = (-5)(-5) = 25
Incorrect. -52 = (-1)(5)(5) = -25 and (-5)2 = (-5)(-5) = 25
Incorrect. -52 = (-1)(5)(5) = -25 and (-5)2 = (-5)(-5) = 25
Simplify and write in exponential form.
\(\large\mathsf{ (5^{3}) (\frac{5^{4} \cdot 5^{0} x^{5}}{3^{2} x^{2} y^{2}}) }\) = ?
- \(\large\mathsf{ (5^{3}) (\frac{1x^{3}}{9y^{2}}) }\)
- \(\large\mathsf{ \frac{5^{12}}{3^{2} x^{3} y^{2}} }\)
- \(\large\mathsf{ \frac{5^{7}x^{3}}{3^{2}y^{2}} }\)
Incorrect. Looks at this solution to find your error:
\(\large\mathsf{ (5^{3}) (\frac{5^{4} \cdot 5^{0} x^{5}}{3^{2} x^{2} y^{2}}) }\) =
\(\large\mathsf{ \frac{5^{3 + 4 + 0}\text{ }x^{5 - 2}}{3^{2}y^{2}} }\) = \(\large\mathsf{ \frac{5^{7}x^{3}}{3^{2}y^{2}} }\)
Incorrect. Looks at this solution to find your error:
\(\large\mathsf{ (5^{3}) (\frac{5^{4} \cdot 5^{0} x^{5}}{3^{2} x^{2} y^{2}}) }\) =
\(\large\mathsf{ \frac{5^{3 + 4 + 0}\text{ }x^{5 - 2}}{3^{2}y^{2}} }\) = \(\large\mathsf{ \frac{5^{7}x^{3}}{3^{2}y^{2}} }\)
That is correct.
Summary
Questions answered correctly:
Questions answered incorrectly:
Exponents
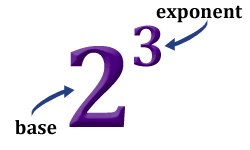
The exponent (also called the power) of a number tells us how many times to multiply a number by itself.
For example: In 23, the power of 3 tells us to multiply the base 2 three times. So, 23 = 2 · 2 · 2 = 8
23 can also be written or read as "2 to the third power," "2 to the power of 3," or "2 cubed."
Here's another example: 52 = 5 · 5 = 25
52 is also seen as "5 to the second power," "5 to the power of 2," or "5 squared."
Different Forms
Exponents make it easier to write and multiply numbers. Example: 96 (exponential form) is easier to write than:
- Expanded Form: 9·9·9·9·9·9
- Standard Form: 96 = 531,441
Now see if you can fill in the missing information. Click each example to fill in the row of answers.
| Exponential Form | Base | Exponent | Expanded Form | Standard Form |
| 74 | 7 | 4 | 7·7·7·7 | 2401 |
| 27 | 2 | 7 | 2·2·2·2·2·2·2 | 128 |
Negative Signs
Let's take a look at this example with negative numbers.
(–2)2 means (–2)(–2) = 4. Remember a negative times a negative equals a positive.
In this next example, let's consider –22. This means –(22) because the Order of Operations (PEMDAS) says that exponents comes before subtraction. So –(22) = –(2·2) = –4.
Ready to practice on some by yourself? Try the examples below:
| Example | Answer |
| –36 | –729 |
| (–15)2 | 225 |
The Product of Powers Property
The Product of Powers Property tells us that when multiplying the same bases raised to powers, we add the powers.
For example:
In expanded form 73 · 75 = (7·7)(7·7·7·7·7) = 78.
Since the bases (7) are the same, add the powers: 7(3 + 5) = 78
Try the examples below:
| Example | Answer |
| 42 · 47 | 49 |
| 93 · 910 | 913 |
The Quotient of Powers Property
The Quotient of Powers Property tells us that when dividing the same bases raised to powers, we subtract the powers.
For example:
In expanded form \(\large\mathsf{ \frac{8^{5}}{8^{3}} }\) = \(\large\mathsf{ \frac{8·8·8·8·8}{8·8·8} }\) = 82
Since the bases (8) are the same, subtract the powers: \(\large\mathsf{ \frac{8^{5}}{8^{3}} }\) = 8(5 - 3) = 82
Try the examples below:
| Example | Answer |
| \(\large\mathsf{\frac{6^{11}}{6^{5}} }\) | 66 |
| \(\large\mathsf{\frac{3^{9}}{3^{5}} }\) | 34 |
The Zero Exponent Property
Any number or term raised to a zero exponent equals 1. So, for example, 30 = 1.
Look at this example: 90 ∙ 91
The Power of a Product Property tells us to add the exponents to get the following: 90 · 91 = 9(0 + 1) = 91 = 9.
But, you could also use the Zero Exponent Property, to get 90 ∙ 91 = 1 ∙ 91 = 1 ∙ 9 = 9
Terms with Different Bases
Now let's look at how to deal with terms that have different bases.
Example
33 · 74 · 35 · 72
Notice that there are two different bases: 3 and 7. First, group the like terms together, to get this: (33 · 35) · (74 · 72)
Notice we use parentheses to keep the terms organized.
Now, using the the Product of Powers Property, we get: (33 + 5) · (74 + 2)
This gives you 38 · 76. Since we were only asked to simplify, this is the final answer. If we were asked to "evaluate" or "find the value of", then we would need to multiply 38 ∙ 76 to get the final answer.
Try the examples below:
| Example | Answer |
| 9 · 67 · 910 · 63 | 911 · 610 |
| 104 · 82 · 105 · 84 | 109 · 86 |
Combining Rules
We can combine these rules. Simplify this expression and write in exponential form.
\(\large\mathsf{ \frac{3^{5} \cdot 3^{6} \cdot 5^{4} \cdot a^{2} \cdot b^{6}}{3^{7} \cdot 5 \cdot a^{5} \cdot b^{2}} }\)
\(\large\mathsf{ \frac{3^{5 + 6} \cdot 5^{4} \cdot a^{2} \cdot b^{6}}{3^{7} \cdot 5 \cdot a^{5} \cdot b^{2}} }\) = \(\large\mathsf{ \frac{3^{11} \cdot 5^{4} \cdot a^{2} \cdot b^{6}}{3^{7} \cdot 5 \cdot a^{5} \cdot b^{2}} }\)
\(\large\mathsf{ 3^{11 - 7} \cdot 5^{4 - 1} \cdot a^{2 - 5} \cdot b^{6 - 2} }\) = \(\large\mathsf{ \frac{3^{4} \cdot 5^{3} \cdot b^{4}}{a^{3}} }\)
Notice that a2 - 5 equals a-3. Remember, the rule of negative exponents? It says that a number (or term) raised to a negative exponent is the reciprocal number (or term) raised to the positive exponent. So, a-3 is equal to \(\small\mathsf{ \frac{1}{a^{3}} }\) which moves it to the denominator in the final answer.
———
Now that you have had some more practice, you should be better prepared for your quiz. If you still do not feel confident about any topics, please contact your teacher for some additional help.
