Helpful Examples
Let’s practice using partial quotients with remainders.
Goal:
Goal:

The example problems below demonstrate the steps to solve division expressions using partial quotients with remainders. Work through each problem, using partial quotients. Then, click each row to reveal the solution.
The powers of 10 when multiplied by your
divisor of 16 are:
160 (16 x 10), 1,600 (16 x 100), and 16,000 (16 x 1,000)
Both 1,600 and 16,000 are too large to be used with a
dividend of 657.
But, 160 is less than 657, so we can subtract groups of 160
to begin calculating for the partial quotient:
Compare your solution to the one below.
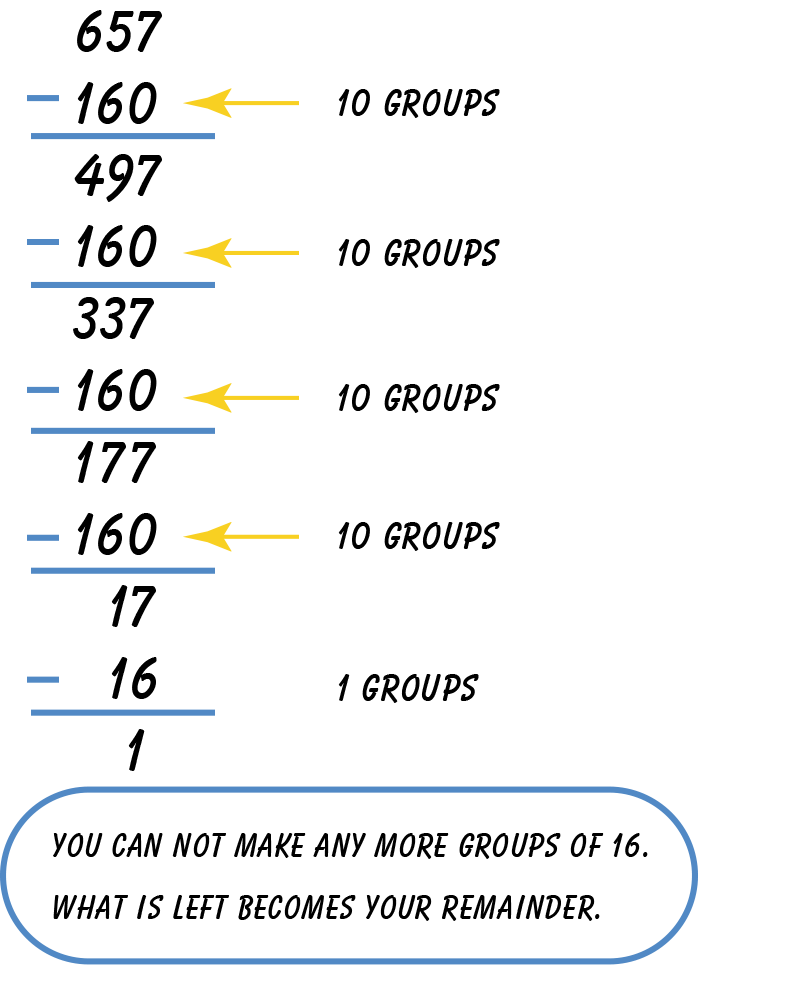
So, what is the final quotient?
Add the groups of your partial quotients:
10 + 10 + 10 + 10 + 1 = 41. This means that there
are 41 whole groups of 16 plus 1 left over, which
will be the remainder. So, 657 ÷ 16 = 41 R1.
The powers of 10, when multiplied by the divisor of 14 are:
140 (14 x 10), 1,400 (14 x 100), and 14,000 (14 x 1,000)
Both 1,400 and 14,000 are too large to be used with a
dividend of 961.
However, 140 is less than 961, so we can begin by
subtracting groups of 140 to start calculating for the
partial quotients.
Compare your solution to the one below.
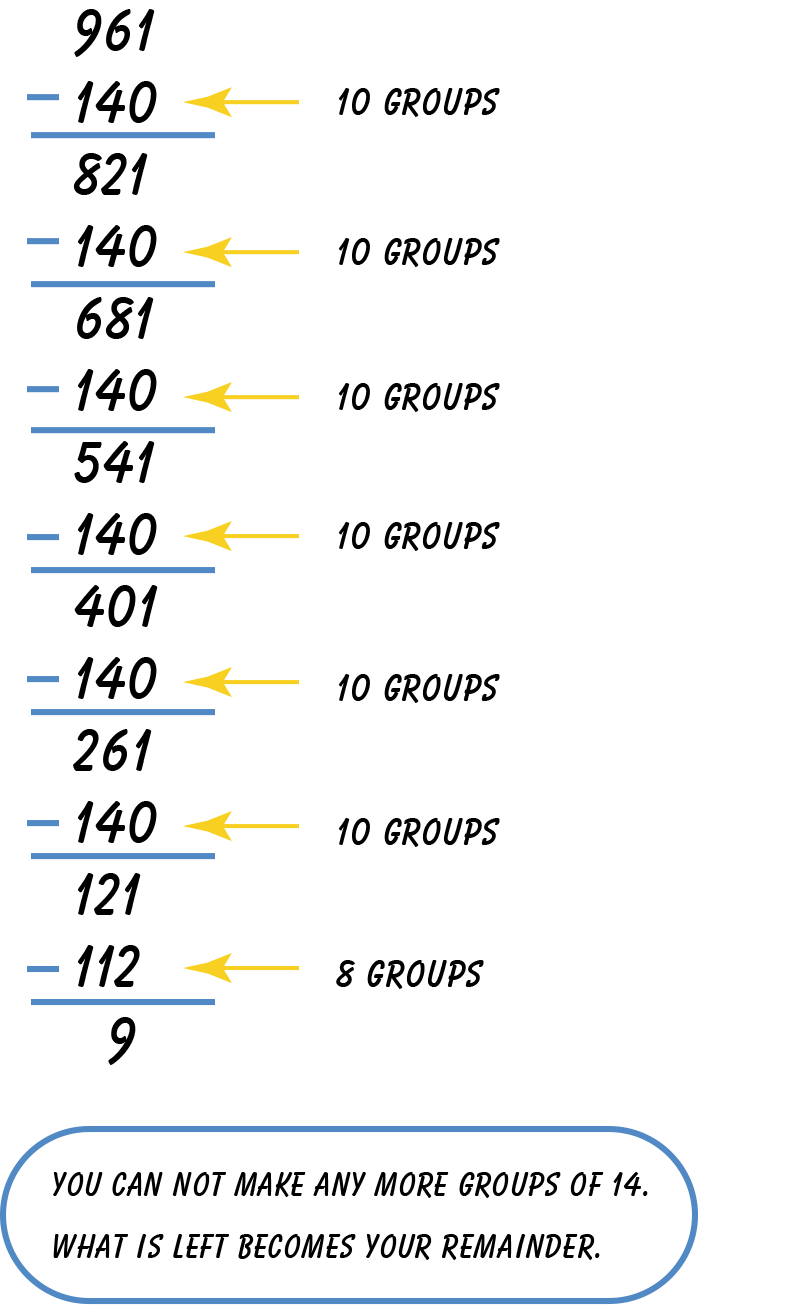
What is your final quotient?
Add the groups of your partial quotients:
10 + 10 + 10 + 10 + 10 + 10 + 8 = 68. This means
that there are 68 whole groups of 14, with 9 left
over, which will be the remainder. So, 961 ÷ 14 =
68 R9.
The powers of 10 when multiplied by your divisor of 37 are:
370 (37 x 10), 3,700 (37 x 100), and 37,000 (37 x 1,000)
Both 3,700 and 37,000 are too large to be used with the
dividend of 1,949.
However, 370 is less than 1,949, so we can begin by
subtracting groups of 370 to start calculating for the
partial quotient.
Compare your solution to the one below.
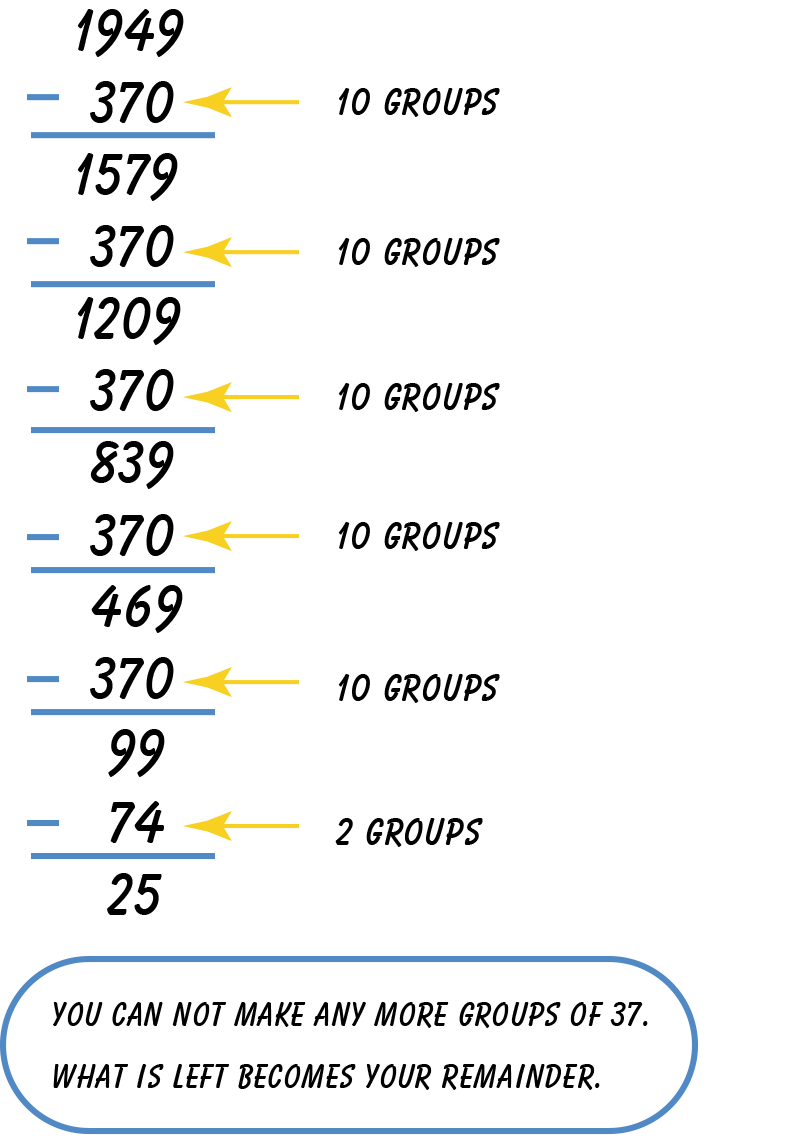
What is your final quotient?
Add the groups of the partial quotients:
10 + 10 + 10 + 10 + 10 + 2 = 52. This means there
are 52 whole groups of 37, with 25 left over
(which will be the remainder). So, 1,949 ÷ 37 = 52
R25.
The powers of 10 when multiplied by your divisor of 87 are:
870 (87 x 10), 8,700 (87 x 100), and 87,000 (87 x 1,000)
87,000 is too large to be used with the dividend of 9,605.
However, 8,700 is less than 9,605, so we can subtract groups
of 8,700 to start calculating for the partial quotients.
Compare your solution to the one below.
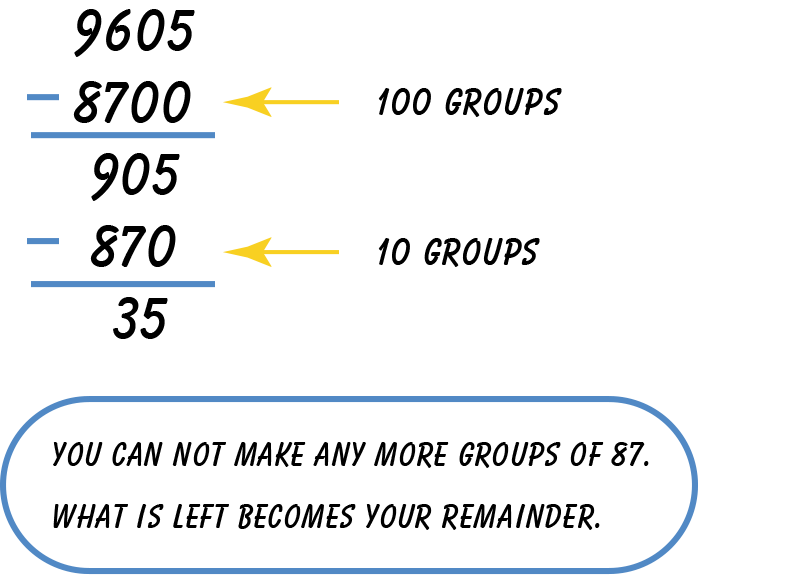
What is your final quotient?
Add the groups of the partial quotients together:
100 + 10 = 110. This means there are 110 whole
groups of 87 with 35 left over. So, 9,605 ÷ 87 =
110 R35.