Sound intensity is the pressure per unit of area of a sound wave. It can be calculated using the power output of a source and how far the listener is from that source.
Sound Intensity
\(\large\mathsf{ I = \frac{P}{A} = \frac{P}{4 \pi r^2} }\)
Use the intensity equation to solve these problems on your own. Check your work when you are done.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
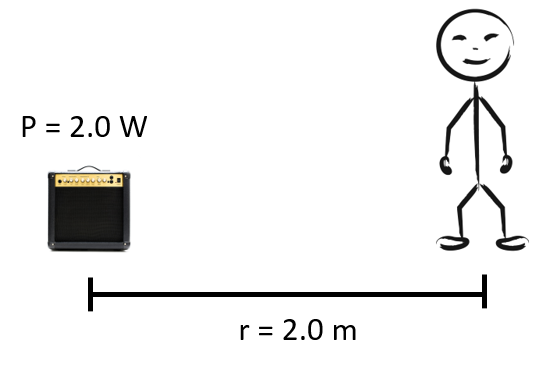
| An amplifier has a power output max of 2.0 W. If you are standing 2.0 meters away from that speaker, what is the sound intensity at that distance at max output? |
|
\(\mathsf{ P = 2.0 \text{ W}}\) \(\mathsf{ r = 2.0 \text{ m} }\) \(\mathsf{ I = ? \text { W/m}^2 }\) |
\(\mathsf{ I = \frac{P}{4 \pi r^2} }\) | \(\mathsf{ I = \frac{2.0 \text{ W}}{4 \pi (2.0 \text{ m})^2} }\) \(\mathsf{ I = 0.040 \text{ W/m}^2 }\) |
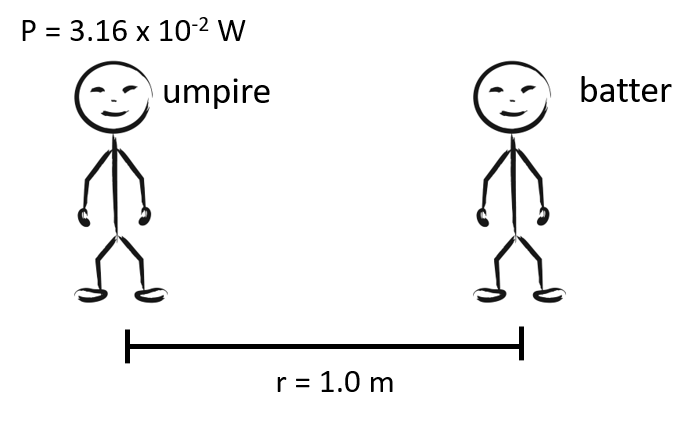
| An umpire yells "strike" when a baseball player misses the ball. His power output is 3.16 x 10-2 W. What intensity does the player hear the umpire if he is standing 1.00 m away? |
|
\(\mathsf{ P = 3.16 \times 10^{-2} \text{ W}}\) \(\mathsf{ r = 1.00 \text{ m} }\) \(\mathsf{ I = ? \text { W/m}^2 }\) |
\(\mathsf{ I = \frac{P}{4 \pi r^2} }\) | \(\mathsf{ I = \frac{3.16 \times 10^{-2} \text{ W}}{4 \pi (1.00 \text{ m})^2} }\) \(\mathsf{ I = 0.00251 \text{ W/m}^2 }\) |
| To a listener that is 25.0 meters away from the platform, hears a symphony orchestra with an intensity of 8.91 x 10-3 W/m2. What is the power output of that symphony? |
|
\(\mathsf{ P = ? \text{ W}}\) \(\mathsf{ r = 25.0 \text{ m} }\) \(\mathsf{ I = 8.91 \times 10^{-3} \text { W/m}^2 }\) |
\(\mathsf{ I = \frac{P}{4 \pi r^2} }\) | \(\mathsf{ 8.91 \times 10^{-3} \text { W/m}^2 = \frac{P}{4 \pi (25.0 \text{ m})^2} }\) \(\mathsf{ P = (8.91 \times 10^{-3} \text { W/m}^2)(4 \pi (25.0 \text{ m})^2) }\) \(\mathsf{ P = 70.0 \text{ W} }\) |