As you may have already guessed, induction and deduction both have important roles in geometry. To make a theorem from scratch, a mathematician gathers data, usually in the form of examples, and uses induction to make a conjecture. Then, he or she uses deduction to prove that conjecture. As a geometry student, you may be given a conjecture and asked to prove (or disprove) it. You might not need induction to prove the conjecture--only deduction. However, creating a list of example can sometimes help you figure out what definitions and theorems you might use to prove the conjecture.
Use the information and examples on these tabs to learn how the two types of reasoning are applied in geometry.
Applying Induction
Applying Deduction
When you apply inductive reasoning in geometry, you use data like the information in the figure below to form a conjecture. The numbers in the figure represent the first 6 triangular numbers: 1, 3, 6, 10, 15, and 21. These numbers are called triangular because each number can be drawn as a equilateral triangle.
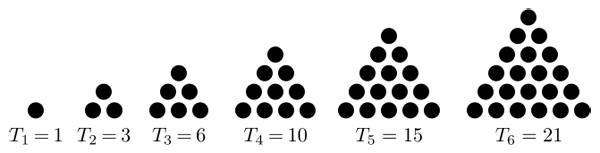
How can we determine the 7th triangular number? Look for patterns, of course! You probably noticed right away that the numbers get larger each time. But by how much? Does the set of equations below help you see the pattern?
1 = 1
1+2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
In each example equation, we take the previous number or solution and add the next highest number to that.
Question
What number should we add to 15 to get the next triangular number?
6 should be added. 15 + 6 = 21
In this example, inductive reasoning led us to identify a pattern in the given list of numbers and then make a strong prediction based on that pattern. See if you can use your understanding of this pattern to predict the 7th triangular number. Write your response in your notebook before you reveal the answer.

1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
In a geometry course, deductive reasoning involves applying both the rules of logic (such as syllogisms and the law of detachment) with known definitions, postulates, and theorems as well as the rules of algebra. Consider this problem.

Known Property: If two angles are vertical angles, then they are congruent.
Problem Given: Angle A and angle B are vertical angles.
What does the process of deduction tell you about angles A and B? Write your response in your journal before you check your answer.

m∠A = m∠B
