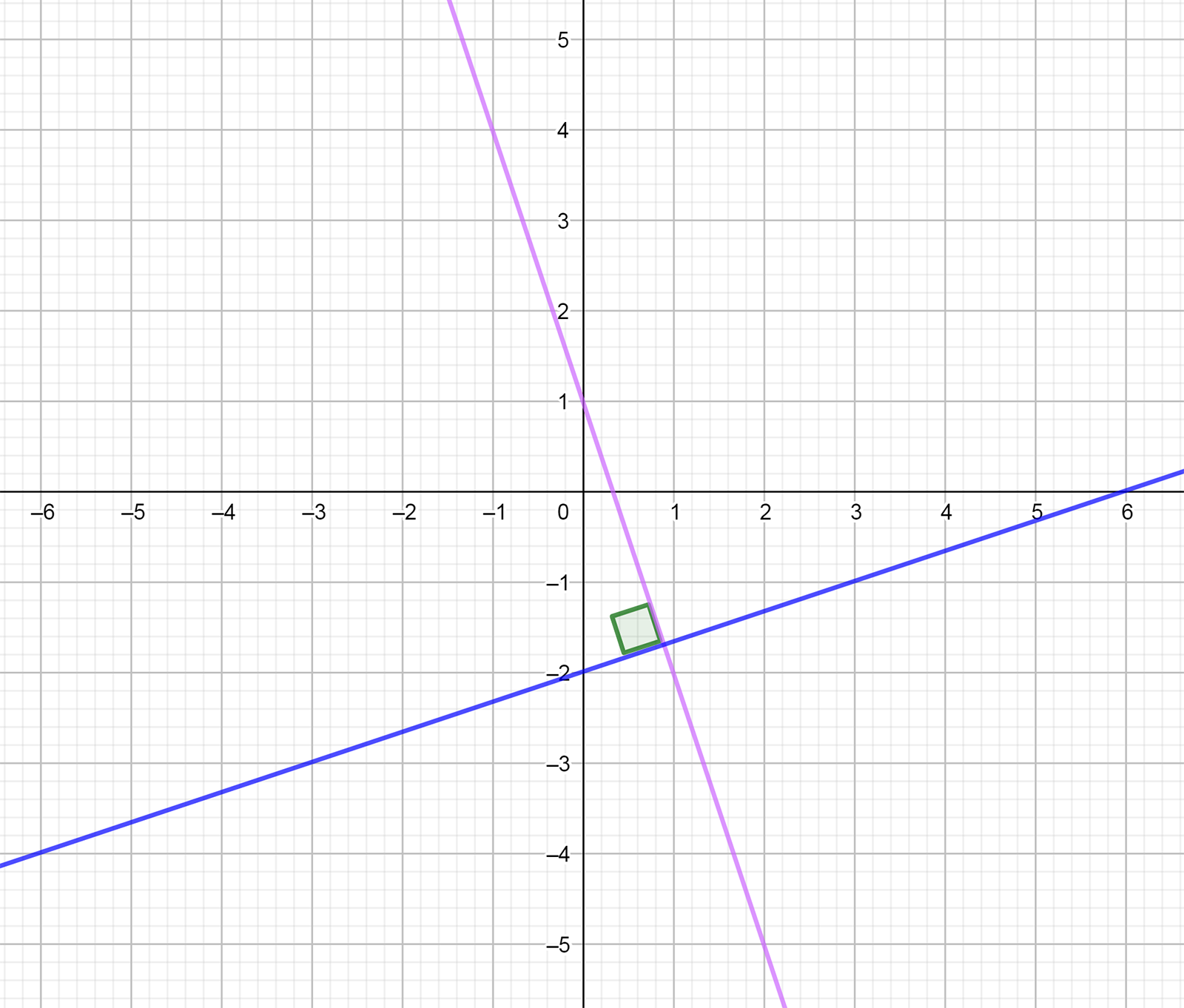
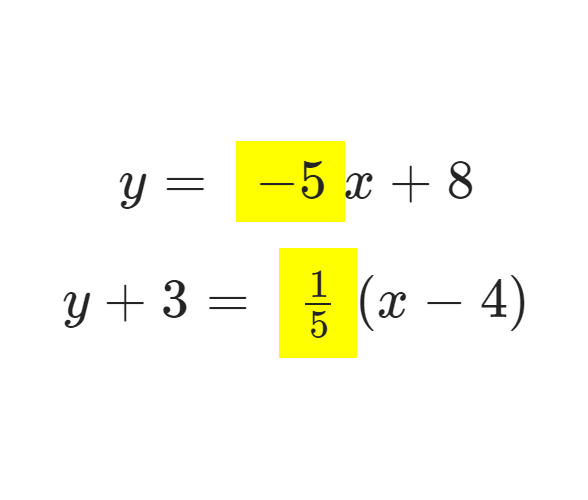Loading...

What are perpendicular lines?

You have learned that parallel lines are special sets of lines that extend forever in each direction and do not touch or intersect. When you look at the equations of parallel lines, their slope values are identical, but their \( y \)-intercept values are different.

Another set of special lines are perpendicular lines. The blue and the green line shown on the graph are perpendicular. A set of perpendicular lines intersects at a \( 90{^\circ} \) angle. When perpendicular lines are represented using an equation, their slopes have values that are opposite reciprocals.

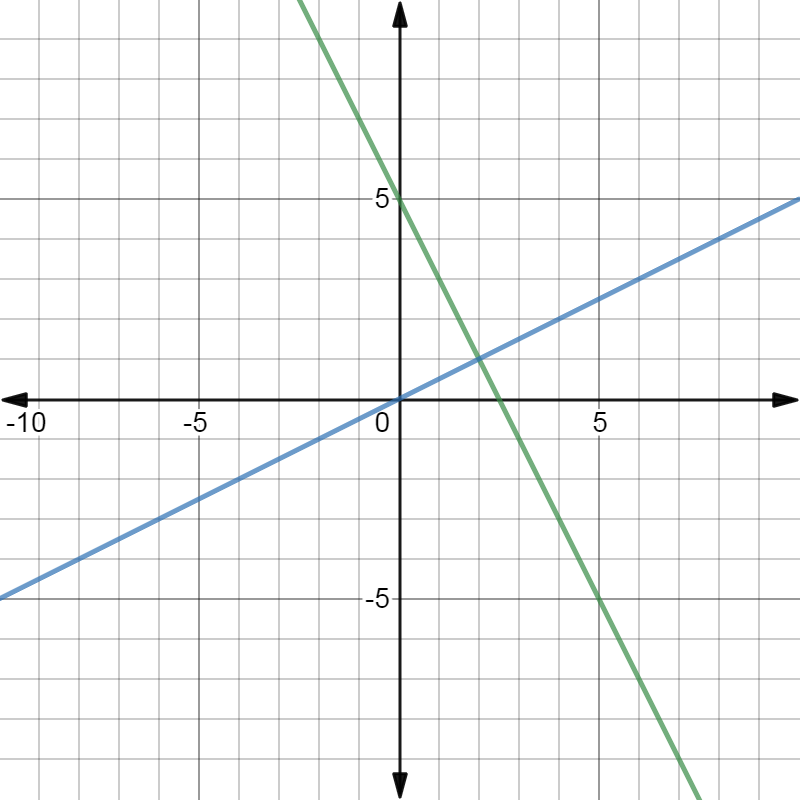
A detailed description of this image follows in the next paragraph.

Graph of two perpendicular lines. One line is blue. The other line is green.

Opposite Reciprocals

A number's opposite reciprocal has the opposite sign of the original number, and the number's numerator and denominator are interchanged. All real numbers except zero have reciprocals. The product of a number and its opposite reciprocal is always \( - 1. \)

For example:

The opposite reciprocal of the number \( 7 \) is \( - \frac{1}{7} \).
The product of these numbers equals \( - 1 \) because \( 7 \cdot - \frac{1}{7} = - 1. \)

The opposite reciprocal of the number \( - \frac{3}{8} \) is \( \frac{8}{3} \).
The product of these numbers equals \( - 1 \) because \( - \frac{3}{8} \cdot \frac{8}{3} = - 1. \)

Every number except 0 has an opposite reciprocal. The number \( 0 \) does not have an opposite reciprocal because the expression \( - \frac{1}{0} \) is undefined. This is an important idea for perpendicular lines because the slope of a horizontal line is \( m = 0 \). Since \( 0 \) has no opposite reciprocal, you cannot express the relationship between an intersecting horizontal and vertical line using opposite reciprocals. Because of this, all the perpendicular lines you will see in this lesson are known as non-vertical perpendicular lines.

Look at the images shown below. Each image represents a set of perpendicular lines. Study each one carefully, then click the image to learn why the set can be described as perpendicular lines.

Graph of two perpendicular lines with a right angle mark showing that the two lines intersect each other at a 90-degree angle. Use enter key to open full-screen view.
Image captioned below. Use escape key to exit full screen view.

This graph contains a pair of perpendicular lines. You know they are perpendicular because they intersect at a \( 90{^\circ} \) angle. Recall that you mark an angle of \( 90{^\circ} \) using a square, as shown by the green square on this graph.

Pattern created by several sets of perpendicular lines. Use enter key to open full-screen view.
Image captioned below. Use escape key to exit full screen view.

The pattern in this fabric features several sets of perpendicular lines. These lines intersect at \( 90{^\circ} \) angles.

Use enter key to open a description of the two equations in this image.

\( \Large y = \ \require{color}\colorbox{yellow}{$ - 5 $}x + 8 \)

\( \Large y + 3 = \ \require{color}\colorbox{yellow}{$ \frac{1}{5} $}(x - 4) \)

These equations represent perpendicular lines because their slope values are opposite reciprocals. The slope of the first line is \( m = - 5, \) and the slope of the second line is \( m = \frac{1}{5} \). The product of \( - 5 \) and \( \frac{1}{5} \) is \( - 1 \).

Recognizing the opposite reciprocal of a number is key to determining if two equations represent perpendicular lines. How well can you identify the opposite reciprocal of a number? Use the activity below to practice. Match the number on the left with its opposite reciprocal on the right.

Great job!