On the previous page, you saw how to solve a real-life problem involving the area of a rectangle. But here are other problems that can be solved using the properties of quadrilaterals. Every quadrilateral also has angles--four of them! Note the role that angles play in the following situation.

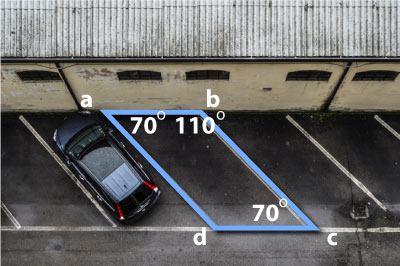
As part of a special youth initiative, you have been asked to design a parking lot for the new recreation center downtown. You decide to make the parking spaces non-rectangular parallelograms to save space and to make turning into the parking spaces easier. To help make the best use of the space available for parking, you need to provide angle measurements to the paint crew who will draw the lines for the parking spaces.
If you know that Angle C is 70°, what strategy can you use to find the measurements of the other 3 angles in the parking parallelogram?
To find missing angles, recall what you've learned about the relationships between a known angle and an unknown angle in a quadrilateral.
Now, work through the following steps to find the missing angles. You'll need to find m∠A, m∠B and m∠D.
|
Angle A (unknown) and Angle C (known to be 70°) are opposite angle pairs.
You still need to find the measurement of ∠B. You may remember from your study of parallelograms that ∠C and ∠B are consecutive angles.
You only have one more angle to figure out, ∠D.
|
Question
What if the measure of ∠C =76 degrees? Find m∠A, m∠B, and m∠D in this scenario.

m∠A =76 degrees (congruent to angle C )
m∠B = 104 degrees (supplement to angle C)
m∠D = 104 degrees (you could use the interior angle sum to find the 4th angle if you know 3 of the angles)