Try working through a problem similar to the one you just saw in the video. Calculate the width of a 60 inch television with a 21:9 aspect ratio. The slides below will help guide you through the steps required to find the missing side in the quadrilateral formed by the television screen.
|
Step 1: Draw a diagram to represent the problem.
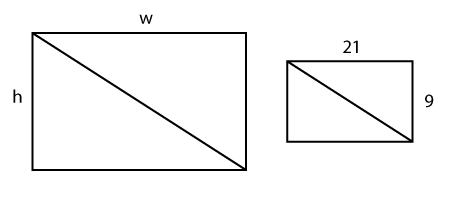
Draw two similar rectangles. One rectangle will represent a TV with the correct aspect dimensions. The other rectangle will represent the 60 inch TV. Draw a diagonal going from the top left to the bottom right on both rectangles. Step 2: Label the height and width of the both rectangles.
Label the width of the smaller rectangle with the first number that appears in the aspect ratio (21). Label the height of the smaller rectangle with the second number from the aspect ratio, (9). Then, label the width of the second rectangle with a w and the height with an h. Step 3: Label the diagonals.
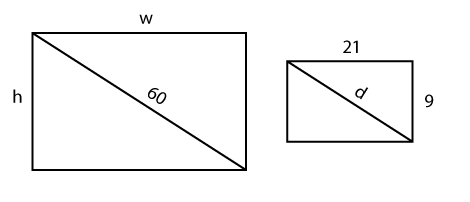
Label the diagonal of the smaller rectangle (representing the aspect ratio) with a d. Label the diagonal of the larger rectangle (the 60 inch TV) as 60. Step 4: Use the Pythagorean Theorem to find the diagonal of the aspect ratio rectangle.
You can think of the diagonal as the hypotenuse and the width and height as legs of a right triangle sitting inside the rectangle. In your notebook, see if you can solve for d using the Pythagorean formula. Then, check your work. \(\mathsf{21^2 }\) + \(\mathsf{9^2 }\) = \(\mathsf{d^2 }\) →
441 + 81 = \(\mathsf{d^2 }\)
522 = \(\mathsf{d^2 }\)
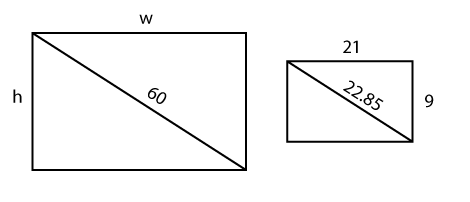
d = \(\mathsf{ \sqrt {522} }\) = 22.85 in
Now, label the aspect diagonal with its length that you just found.
Step 5: Set up a proportion and solve for the desired dimension.
Make a ratio of diagonal to width using the labels on the smaller rectangle (the aspect ratio TV). Then solve for the measure of w in the larger rectangle (the one with the 60 inch diagonal). Ratio: \(\mathsf{ \frac{22.85}{21} }\) = \(\mathsf{ \frac{60}{w} }\) To solve the proportion, cross multiply:
|