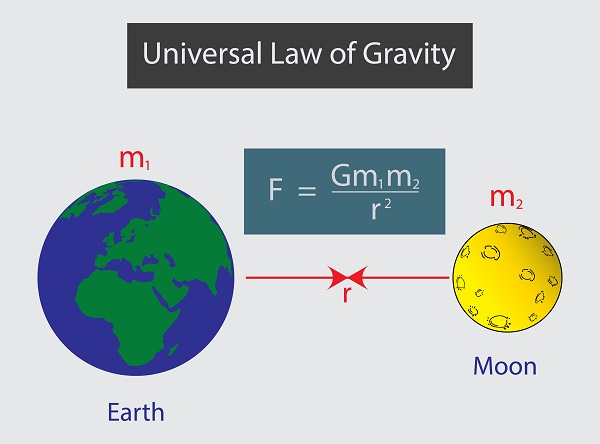
Newton's Law of Universal Gravitation shows the magnitude of force between two objects a certain distance apart.
Newton's Law of Universal Gravitation
\(\large\mathsf{ F_g = \frac{Gm_1m_2}{r^2} }\)
...where G is the universal gravitational constant of 6.673 x 10-11 Nm2/kg2, m1 is the mass of the first object, m2 is the mass of the second object, and r is the distance between their centers.
Using this equation is a matter of substituting what you know into the equation and solving for the unknown. Take for example, finding the force of gravity on a 95.0 kg astronaut that is 225 km above the surface of the Moon. If the mass of the moon is 7.36 x 1022 kg, and the radius of the Moon is 1.737 x 106 m, you substitute the known information into the equation. Keep in mind, though, that you must take into consideration that the distance between the center of the objects is the radius of the Moon plus the astronaut's altitude.
\(\mathsf{ F_g = \frac{Gm_1m_2}{r^2} }\)
\(\mathsf{ F_g = \frac{(6.673 \times 10^{-11} \text{ Nm}^2 \text{/kg}^2)(7.36 \times 10^{22} \text{ kg})(95.0 \text{ kg})}{(1.737 \times 10^{6} \text{ m} + 2.25 \times 10^{5} \text{ m})^2} }\)
\(\mathsf{ F_g = \frac{4.67 \times 10^{14} \text{ Nm}^2}{(1.962 \times 10^{6} \text{ m})^2} }\)
\(\mathsf{ F_g = \frac{4.67 \times 10^{14} \text{ Nm}^2}{(1.962 \times 10^{6} \text{ m})^2} }\)
\(\mathsf{ F_g = 121 \text{ N} }\)
Question
What's the difference between finding the force of gravity and the acceleration of gravity using Newton's Universal Law of Gravitation?
Since we know by Newton's Second Law, that weight is equal to mass times the acceleration of gravity, Newton's Universal Law of Gravitation can be altered to show the acceleration of gravity on any mass by a planetary object:
\(\mathsf{ F_g = \frac{GMm}{r^2} }\)
\(\mathsf{ \cancel{m}g = \frac{G M \cancel{m}}{r^2} }\)
\(\mathsf{ g = \frac{GM}{r^2} }\)
