True or false: a dilation produces congruent figures?
- true
- false
False. Since a dilation changes the size of the figure, it produces similar (not congruent) figures.
False. Since a dilation changes the size of the figure, it produces similar (not congruent) figures.
True or false: a reflection produces congruent figures?
- true
- false
True. A reflection preserves the size and shape of the original figure.
True. A reflection preserves the size and shape of the original figure.
Are the following two figures congruent or similar?
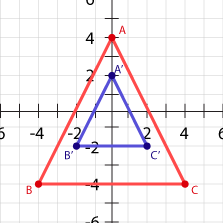
- congruent
- similar
One of these figures is a dilation of the other, so they cannot be congruent.
One of these figures is a dilation of the other, so they cannot be congruent.
Are the following two figures congruent or similar?
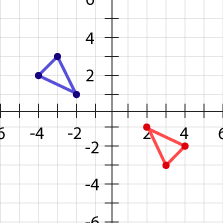
- congruent
- similar
One of these figures was rotated to create the other, so the two are congruent.
One of these figures was rotated to create the other, so the two are congruent.
The vertices of a rectangle are as follows:
(2, 1), (2, 4), (6, 4), and (6, 1)
If the rectangle is dilated by a scale factor of 3, which of the following is the correct list of new vertices?
- (2, 1), (6, 12), (18, 12), (6, 1)
- (6, 1), (6, 4), (18, 4), (18, 1)
- (6, 3), (6, 12), (18, 12), (18, 3)
- (2, 3), (2, 12), (6, 12), (6, 3)
To dilate a figure, you must multiply each of its coordinate points by the given scale factor.
To dilate a figure, you must multiply each of its coordinate points by the given scale factor.
To dilate a figure, you must multiply each of its coordinate points by the given scale factor.
To dilate a figure, you must multiply each of its coordinate points by the given scale factor.
Is it true or false that the shaded triangle below is a dilation of the empty triangle by a factor of \(\small\mathsf{ \frac{1}{2} }\)?
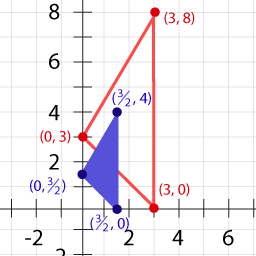
- true
- false
The points for the vertices of the empty triangle were mutliplied by \(\small\mathsf{ \frac{1}{2} }\) to produce the vertices of the shaded triangle.
The points for the vertices of the empty triangle were mutliplied by \(\small\mathsf{ \frac{1}{2} }\) to produce the vertices of the shaded triangle.
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
