In a geometry course, you may be given a figure and asked to draw a dilation with a particular scale factor. How can you accomplish this task correctly? What steps would help you draw an accurate dilated figure? Let's work through an example so that you can see the procedure performed, step by step.
Suppose you were required to dilate, or resize, this shape by a factor of 2.
What will the new triangle look like? Click through these slides, paying close attention to the tasks involved at each step.
Identify the Points
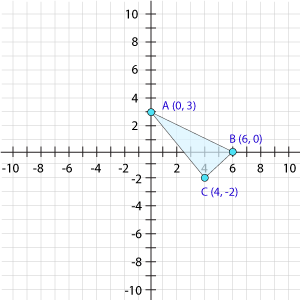
As you know, any triangle consists of three angles. The first step in dilation is to identify the coordinate points of each angle's vertex. Create a copy of the graph above on your own graph paper and label the coordinate points for vertices A, B, and C.
A (0,3); B (6,0); (4,-2)
Create New Points
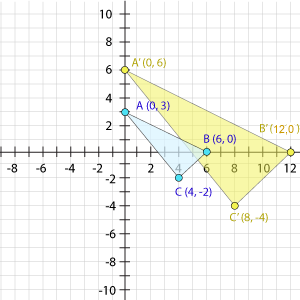
The next step is to increase each of the coordinate points by a factor of 2. To do this, multiply each number by the 2 (the scale factor for this problem) to arrive at the coordinates for a dilated shape. When you multiply each coordinate by 2, these are the new coordinates.
Draw a Dilated Triangle
Finally, make the new coordinates the vertices (A', B' and C') for a new larger triangle. Place the points on the coordinate plane, label them, and connect the points to create a triangle. |
Question
What type of math computation was used to dilate the triangle on this page?