Transformations can be used to prove that two shapes are similar. Two shapes are similar if there is a combination of translations, reflections, rotations, and/or dilations that can transform one shape into the other. For example:
Two random circles, A and B, are shown on the following graph:
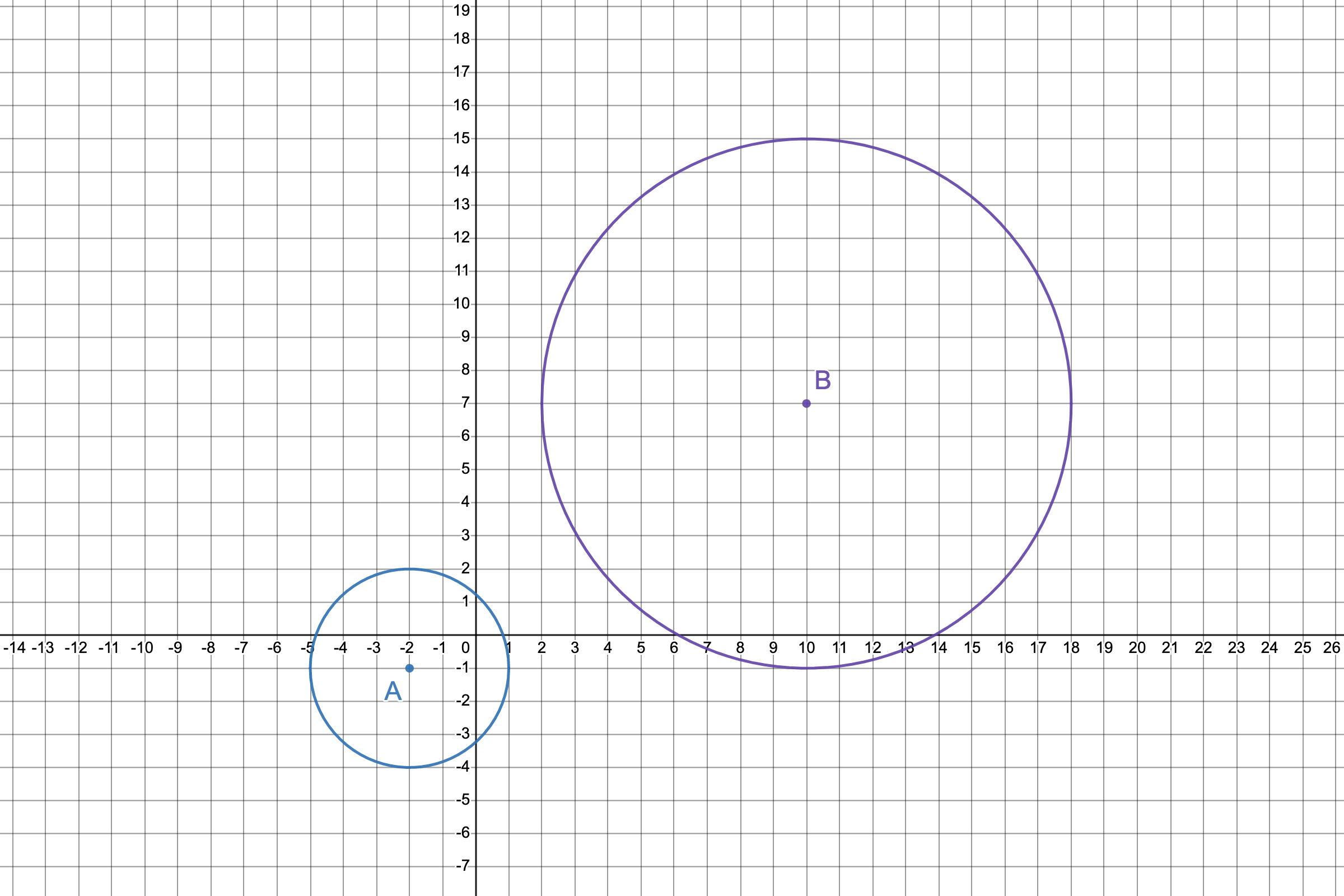
To prove that they are similar, Circle A must be able to be transformed into Circle B. This process can begin by translating Circle A from its center 12 units to the right and 8 units up to align with Circle B’s center, shown here:
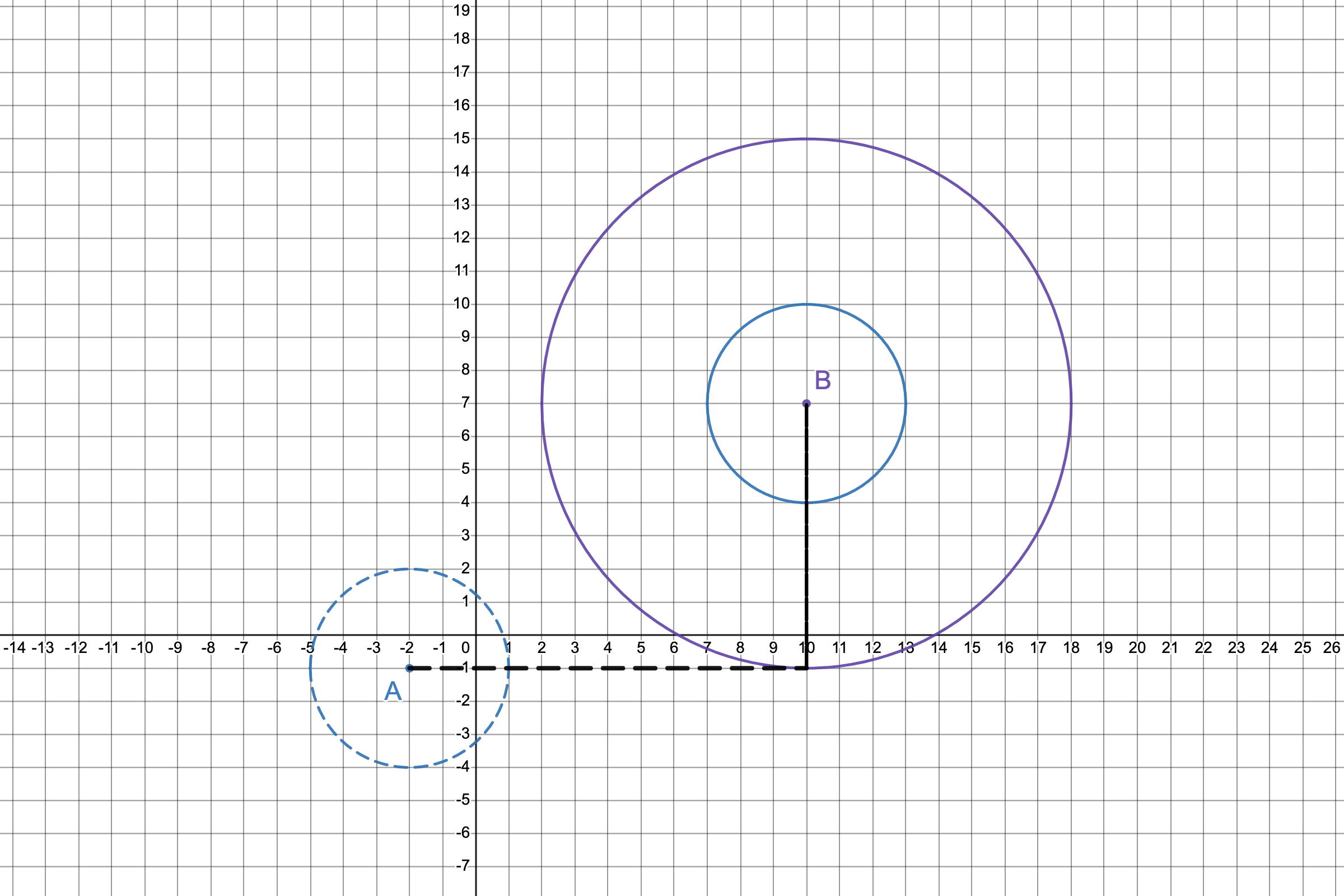
Now that the circles share a center, the next transformation on Circle A must be a dilation since the circles’ sizes are different. To perform this, a scale factor must first be found. Since the size of a circle is dependent on its radius, divide the radius of Circle B by the radius of circle A to determine the scale factor.
The radius of Circle B is 8, and the radius of Circle A is 3. This means that the scale factor is \({ \frac{8}{3} ≈ 2.67 }\) . Multiply the radius of Circle A by the scale factor to get the final transformed circle.
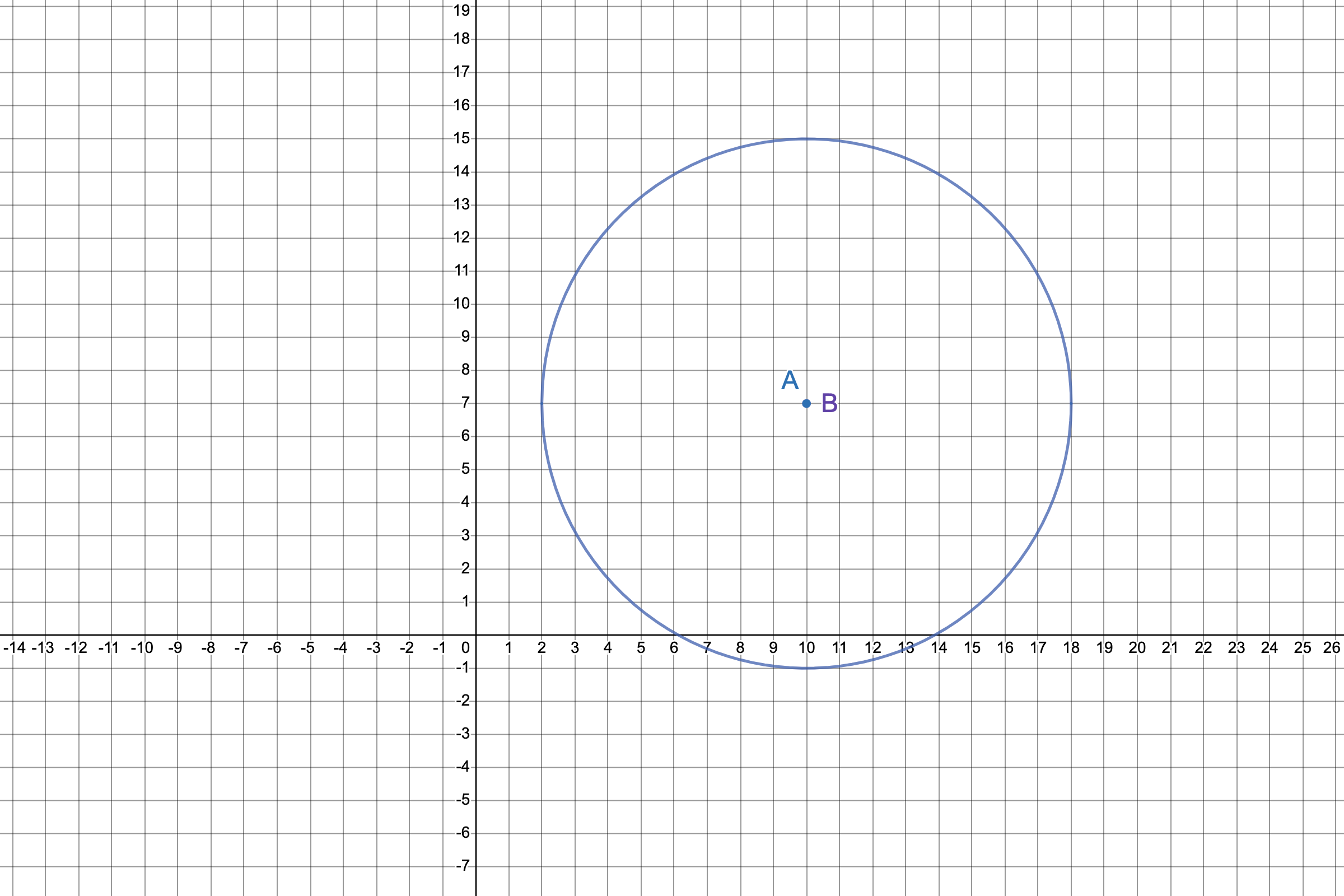
Since Circle A was able to be transformed into Circle B, the two are similar. As these were two random circles, this process can be performed on any other two random circles getting the same results, thus proving that all circles are similar.
This is not the only way to prove that circles are similar. Another method is using the ratio of a circle’s circumference to its diameter; similar circles will have equal ratios. See if you can answer the following question using this knowledge and the information above.
Question:
Prove that a circle with a circumference of 47.1 and a diameter of 15 is similar to a circle with a circumference of 78.5 and a diameter of 25.
To prove that these circles are similar, determine if they have the same ratio between each of their circumferences and diameters.
\({ \frac{47.1}{15} = 3.14 }\)
\({ \frac{78.5}{25} = 3.14 }\)
Since \({ \frac{47.1}{15} =\frac{78.5}{25} }\), the two circles are proven similar. The scale factor from the smaller circle to the larger circle is \({ \frac{25}{13} =\frac{5}{3} }\).
