As you know if you've ever played with blocks, a shape can be moved, flipped, and rotated so that it ends up in a different position than it started in—without changing its shape or size. When a geometric shape is moved, flipped, or rotated, it's called a transformation. Dilation is also a type of transformation, but it differs from most other types in one key way. Study the tabs below to learn how different transformations produce different relationships between shapes.
Translation
Reflection
Rotation
Dilation
A translation is a transformation that moves or slides a figure to a new location. Every single point of the original figure moves the same distance so that the figure's shape and size are preserved. If both the shape and size of the figure stay the same, what kind of relationship does translation produce? What word would describe the two figures?
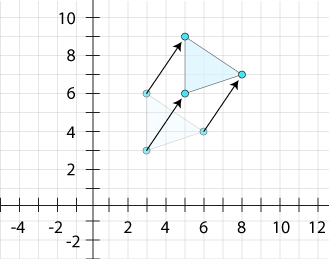
The original figure and the translated figure are congruent.
A reflection, sometimes called a flip, is a mirror image of a figure across some line. Think of standing in front of a mirror and seeing your reflection. The new figure is an exact copy of the original figure. What kind of relationship is produced by reflection?

Congruence. If one shape is a reflection of another, the two shapes are congruent.
A rotation, sometimes called a turn, is a transformation that turns a figure around a fixed point. Why are these two shapes considered congruent—not similar?
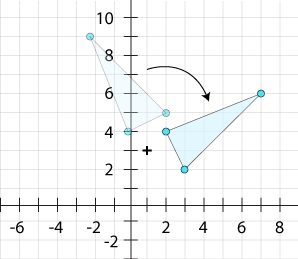
The original figure and the transformation have the same size and shape, which makes them congruent. To be similar, the two shapes would have to be different sizes.
Dilation is the only transformation that produces similar figures rather than congruent ones. How is dilation different from translation, reflection, and rotation?
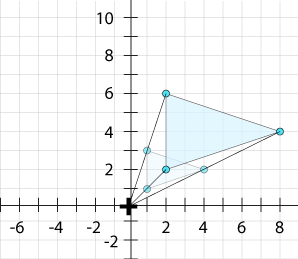
Translations, reflections, and rotations preserve the shape and size of a figure so that the original figure and the transformed figure are congruent. Dilation, though, preserves the shape but not the size of the figure.
