Loading...

What can you use to prove your claim about a set of triangles is true?

In legal matters, to prove that a conjecture is true, you don't need to supply every possible piece of evidence to be found. Some types of evidence, such as a DNA match, are considered proof on their own—without the need for other evidence.

To prove a conjecture related to math, you don't need to present every possible example—which is fortunate because some conjectures would have an infinite number of examples! In geometry, to prove two triangles are congruent, we can use properties and theorems as evidence. By definition, these facts have already been proved and can be used to prove—or disprove—other statements.

For an example, let's return to our two statements about congruent triangles.

The triangles have three sets of congruent (of equal length) sides. 
The triangles have three sets of congruent (of equal measure) angles.

There are five different ways to sufficiently prove any two triangles are congruent. You know these ways as the properties of congruent triangles.

SSS side, side, side   If three sides of one triangle are the same length as three sides of another triangle, the triangles are congruent.
SAS  side, angle, side If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
ASA  angle, side, angle  If two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
AAS  angle, angle, side   If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
HL hypotenuse, leg   If the hypotenuse and leg of one right triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.

As you can see in the table above, if we know that two triangles are congruent, then we know some important pieces of information about their sides and angles. Let's spend a little more time analyzing congruent triangles. See if you can analyze the triangles below using the properties in the table. Answer the question beneath each image, citing the property from the table above that supports your claim. When you get to the last screen, compare your answers to ours. 

Suppose \(\small\mathsf{ \Delta{ABC} \cong \Delta{DEF}}\). What is the relationship between the angles of triangles ABC and DEF? Copy and paste the property that applies.

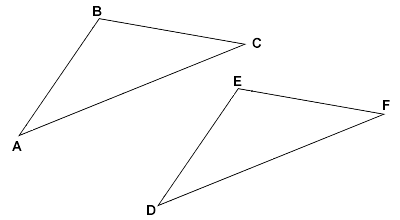
What is the relationship between the sides of triangles ABC and DEF?

Suppose we are given the information \(\small\mathsf{ \Delta{JMK} \cong \Delta{PRQ}}\). What is the relationship between the angles of triangles JMK and PRQ? Copy and paste the property that applies.

What is the relationship between the sides of triangles JMK and PRQ? Copy and paste the property that applies.

Your Responses Sample Answers

When two triangles are congruent, their corresponding angles are congruent. In these triangles, the following is true.
∠A ≅ ∠D
∠B ≅ ∠E
∠C ≅ ∠F

When two triangles are congruent, their corresponding sides are congruent. In these triangles, the following is true.
\(\small\mathsf{ \overline{AC} \cong \overline{DE} }\)
\(\small\mathsf{ \overline{AB} \cong \overline{DE} }\)
\(\small\mathsf{ \overline{BC} \cong \overline{EF} }\).

When two triangles are congruent, their corresponding angles are congruent. The following is true.
∠J ≅ ∠P
∠M ≅ ∠R
∠K ≅ ∠Q

When two triangles are congruent, their corresponding sides are congruent. The following is true.
\(\small\mathsf{ \overline{JK} \cong \overline{PQ} }\)
\(\small\mathsf{ \overline{KM} \cong \overline{QR} }\)
\(\small\mathsf{ \overline{JM} \cong \overline{PR} }\)

Question

Which property is NOT sufficient, on its own, to prove that two triangles are congruent?

SSA