If you can prove that two triangles are congruent, you can prove that two triangles are similar—if you remember the properties that allow us to prove triangle similarity. Try to recall these properties. Jot the list down in your notebook before clicking the Show Me button below to see if you remembered correctly.

Work through the following tabs to see an example of an informal proof of similarity and work through some practice problems.
Example
Problem
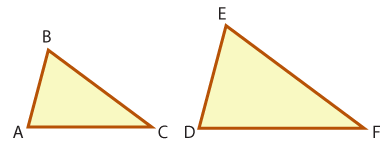
Given: \(\small\mathsf{ \frac{AB}{DE} = \frac{BC}{EF}, \angle{B}\cong\angle{E} }\)
Prove that \(\small\mathsf{ \Delta{ABC}}\) ∼ \(\mathsf{ \Delta{DEF}}\)
Let's work through this proof step by step. Click each step to see it demonstrated.
| Step 1 |
First, we need to identify what is given. We are told the following: \(\mathsf{ \frac{AB}{DE}}\) = \(\mathsf{ \frac{BC}{EF}}\) and ∠B ≅ ∠E |
| Step 2 | Next, we need to decide which similarity property we can use based on the information we are given. Since we know that two corresponding sides are in the same ratio and the included angles are congruent, these triangles are similar by the SAS similarity postulate. |
| Step 3 | Finally, go through your work and make sure that you have not missed any important information. |
Now it's your turn to try a problem. Write an informal proof to show \(\small\mathsf{ \Delta{GIH}}\) ∼ \(\small\mathsf{ \Delta{KLJ}}\). Then click the Show Me button to check your work.
Given: \(\small\mathsf{ \angle{G}\cong\angle{K}, \text{ and } \angle{I}\cong\angle{L} }\)
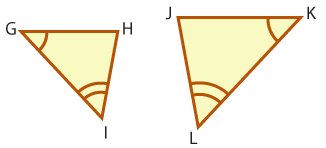

We are given the following information:
∠G ≅ ∠K
∠I ≅ ∠L
Since two corresponding angles are congruent, these two triangles are similar by the AA similarity property.
