Remember, you can't just tell someone something is true—you need to provide evidence, and in geometry, that evidence takes the form of a proof. Before you try writing some proofs on your own, let's review the steps for tackling an informal proof problem.
| Identify what information is given. |
| Determine which property of triangle congruence can be used. Is it SSS, SAS, ASA, AAS, or HL? |
| Write the informal proof step by step, showing all the important details. |
| Go back and read through your proof to make sure you didn't leave anything out. |
Can you prove that the following triangles are congruent? Answer each of the questions below. When you get to the last screen, compare your answers to the ones that are given.
Write an informal proof to show that \(\small\mathsf{ \Delta{ABC} \cong \Delta{DEF}}\)
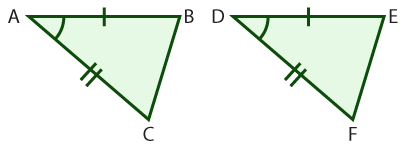
Write an informal proof to show that \(\small\mathsf{ \Delta{ABC} \cong \Delta{DEF}}\)
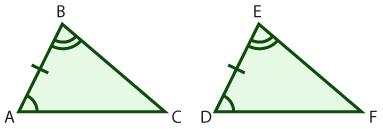
| Your Responses | Sample Answers |
|---|---|
| We are given the following information based on the triangles: \(\small\mathsf{ \angle{A} \cong \angle{D} }\) \(\small\mathsf{ \overline{AB} \cong \overline{DE} }\) \(\small\mathsf{ \overline{AC} \cong \overline{DF} }\) Since two corresponding sides and an included angle are congruent, triangle ABC and DEF are congruent by the SAS property. |
|
| We are given the following information based on the triangles: \(\small\mathsf{ \angle{A} \cong \angle{D} }\) \(\small\mathsf{ \angle{B} \cong \angle{E} }\) \(\small\mathsf{ \overline{AB} \cong \overline{DE} }\) Since two corresponding angles and an included side are congruent, these triangles are congruent by the ASA property. |
