We've talked about the conjectures that people make in everyday life and how these types of statements are similar to some of the statements used in geometry. What conjectures can you reasonably make, based on the image below?

Study each of the conjectures in the activity below, and decide if the statement is likely to be true based on the information in the image. For each question, write a sentence evaluating the conjecture. Then compare your answers to ours at the end of the activity.
The man in the photo is a soccer fan. Is this a reasonable conjecture to make?
This man enjoys the sport of soccer. Reasonable conjecture?
What about This man supports the USA soccer team?
The man in the photo plays soccer for the USA national soccer team. Is this one reasonable?
| Your Responses | Sample Answers |
|---|---|
| This is a reasonable conjecture because the man is holding a soccer ball. | |
| This seems reasonable as he has a smile on his face while holding a soccer ball. | |
| Because he is wearing a USA soccer team jersey, it is reasonable to believe that he supports Team USA. | |
| While it is possible, it's not very reasonable to assume that just because the man is wearing a jersey he is a member of Team USA. Many fans all across America wear this jersey to support our team without actually being players on the team. |
Now, let's use conjecture to prove two triangles are congruent. In the triangles below there are three conjectures given to us that are true.
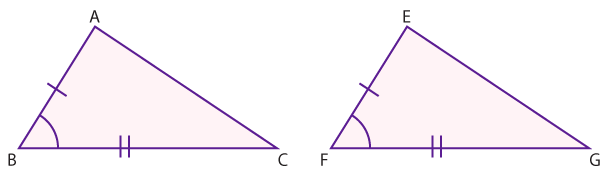
\(\small\mathsf{ \angle{B}\cong\angle{F} }\)
\(\small\mathsf{ \overline{AB}\cong\overline{EF} }\)
\(\small\mathsf{ \overline{BC}\cong\overline{FG} }\)
Any one of these conjectures alone is not enough to prove \(\small\mathsf{ \Delta{ABC} \cong \Delta{EFG}}\). However, given all three conjectures, it can be proved conclusively.
Question
Which of these theorems proves \(\small\mathsf{ \Delta{ABC} \cong \Delta{EFG}}\)?
A) SSS
B) SAS
C) SSA
D) ASA
The SAS (side angle side) theorem proves that the two triangles are congruent.
