Read through the situations below. Draw a free-body diagram in your notes and find the net force acting on the object. Click on each part of the chart below to check your work.
| Problem | Free-Body Diagram | Net Force |
|---|---|---|
| A man pushes a broken-down car with a force of 150 N directly East. The force of gravity on the car is 10,500 N and the force of the ground on the car is also 10,500 N. What is the net force acting on the car? | 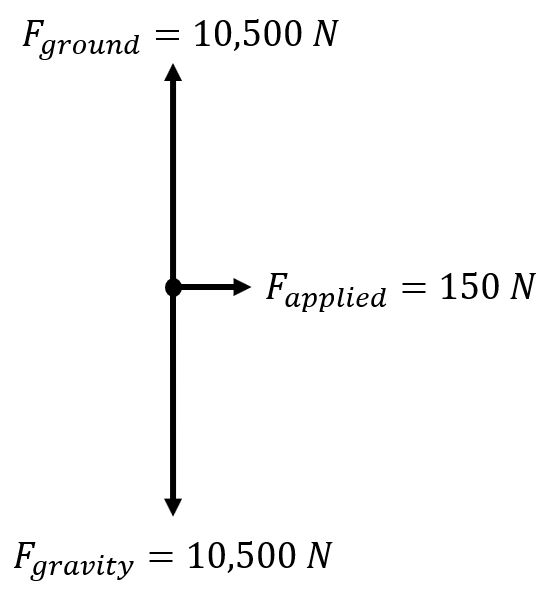 |
The magnitude of the force of gravity and the force of the ground on the car are the same, thus they cancel each other out. The only force that is left is the force applied on the car by the man. \(\small\mathsf{ \overrightarrow{F_{net}} = 150 \text{ N} }\) |
| Two people are pushing on a Volkswagen Bug. The force of gravity on the car is 13,345 N. One person applies a force to the right, of 160.0 N, while the other person applies 205.0 N, in the opposite direction. What is the net force on the Volkswagen Bug? | 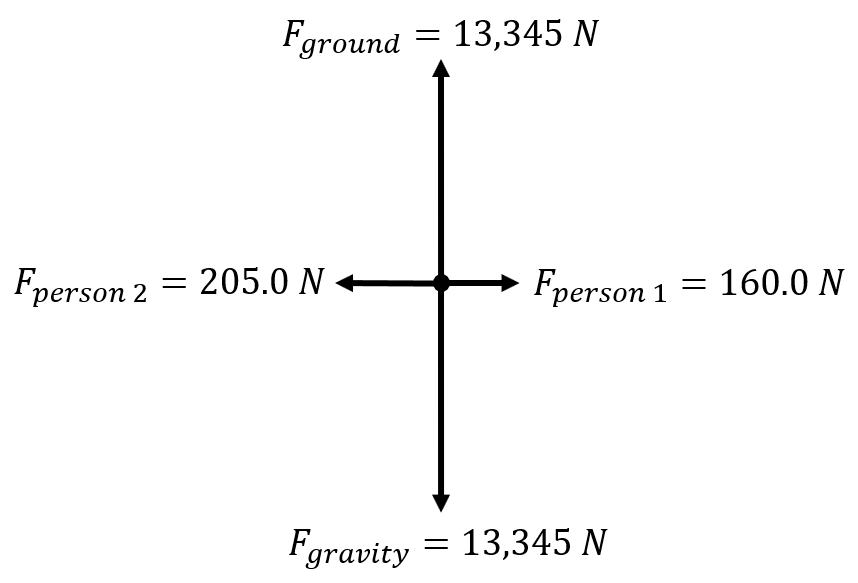 |
The magnitude of the force of gravity and the force of the ground on the car are the same, thus they cancel each other out. The only forces left are in the horizontal direction. \(\small\mathsf{ \overrightarrow{F_{net}} = -205.0 \text{ N} + 160.0 \text{ N} = -45 \text{ N} }\) |
| A woman is standing on a paddle board. By paddling, she causes an average force of 17.0 N to be applied to the raft in the direction due east. The wind also exerts a force on the raft. This force has a magnitude of 15.0 N and points due north. What is the net force on the raft? | 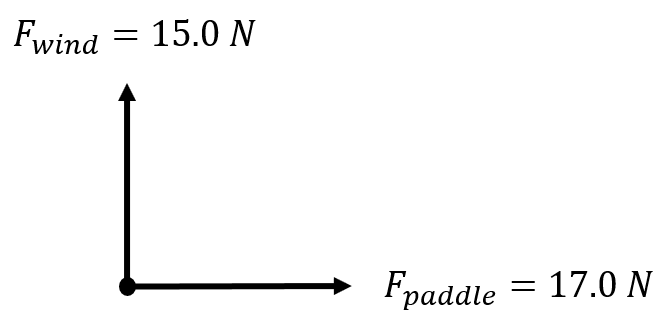 |
Since the two forces are at right angles to one another, add them tip to tail (creating a right triangle). Magnitude: \(\small\mathsf{ c^2 = (17.0 \text{ N})^2 + (15.0 \text{ N})^2 }\) \(\small\mathsf{ c = \sqrt{514 \text{ N}^2} = 22.7 \text{ N}}\) Direction: \(\small\mathsf{\tan{\theta} = \frac{15.0 \text{ N}}{17.0 \text{ N}}}\) \(\small\mathsf{\theta = 41.4° }\) |
| Two people are pushing a stalled car that has a force of gravity of 9,560 N. One person applies a force of +209 N to the car, while the other person applies +289 N, in the same direction. A third force -184 N (friction) acts opposite these forces. | 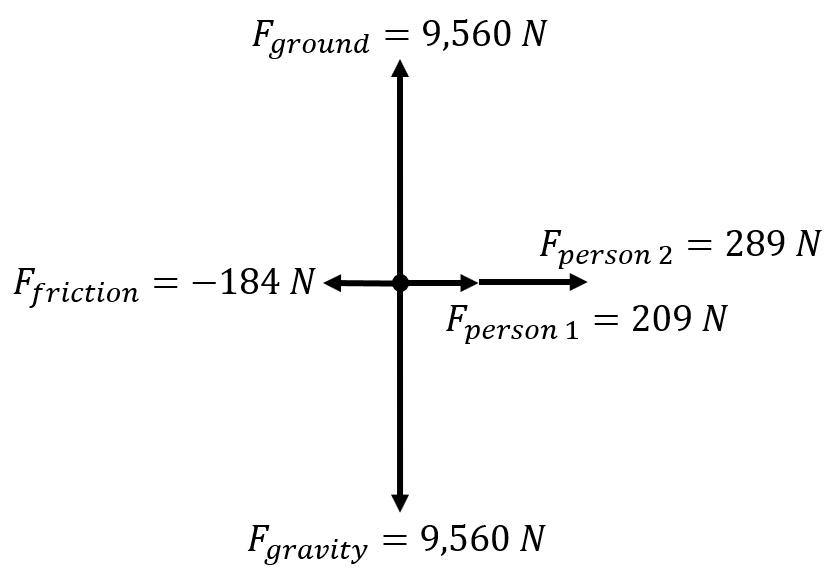 |
The magnitude of the force of gravity and the force of the ground on the car are the same, thus they cancel each other out. The only forces left are in the horizontal direction. \(\small\mathsf{ \overrightarrow{F_{net}} = -184 \text{ N} + 209 \text{ N} + 289 \text{ N} = 314 \text{ N} }\) |
| A man and a dog are fighting over a chew toy. The man pulls up and to the right with a force of 14 N at 10° and the dog pulls up and to the left with 7 N of force at 15°. The dog toy accelerates horizontally only. What is the net force on the dog toy? | 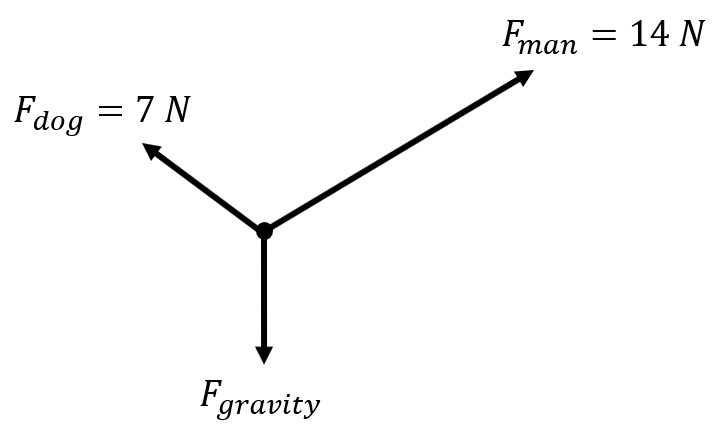 |
If the dog toy accelerations only horizontally, we only need to pay attention to the horizontal components of force. The vertical components of force would have to cancel each other. \(\small\mathsf{ \overrightarrow{F_{net}} = 7(\cos{165°}) \text{ N} + 14(\cos{10°}) \text{ N} = -6.761 \text{ N} + 13.787 \text{ N} = 7.03 \text{ N} \approx 7 \text{ N} }\) |
