Most people need to practice quite a lot with writing informal proofs before the task comes easily to them. Click through the slides below to review the steps involved before writing some informal proofs of you own.
|
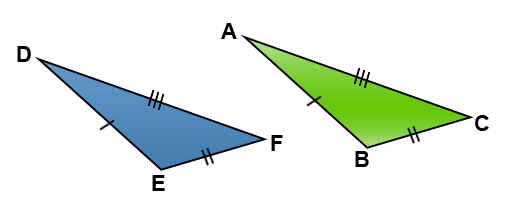
Prove that triangles DEF and ABC are congruent.
Step 1: Write a sentence that identifies two corresponding sides that are congruent. Side \(\small\mathsf{ \overline{DE} }\) is congruent to \(\small\mathsf{ \overline{AB} }\). Prove that triangles DEF and ABC are congruent.
Step 2: Write a sentence that identifies two more corresponding sides that are congruent. Side \(\small\mathsf{ \overline{EF} }\) is congruent to \(\small\mathsf{ \overline{BC} }\). Prove that triangles DEF and ABC are congruent.
Step 3: Write a sentence that identifies the two remaining corresponding sides as congruent. Side \(\small\mathsf{ \overline{FD} }\) is congruent to \(\small\mathsf{ \overline{CA} }\). Prove that triangles DEF and ABC are congruent.
Step 4: Write a sentence that explains which property you just used to show the two triangles were congruent. These two triangles are congruent by the SSS property. |
Now try constructing some informal proofs of your own, using the one above as a model. In your notebook, write an informal proof for each the following problems. When you have written your proof, click the Answer button to check your work.
Problem 1
Problem 2
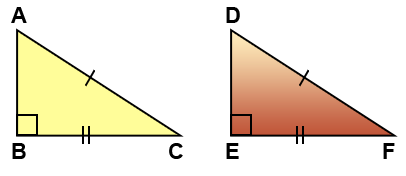
Write an informal proof to show that the two triangles above are congruent.
Since these are right triangles you can use HL.
|

Write an informal proof to show that the two triangles above are congruent.
|