Now let's take a look at two problems involving transversals. To solve these problems, you will need to use the angle properties you learned on the previous pages to find the missing angle measurements.
Problem 1
Problem 2
What are the measures of angles 1 and 2?
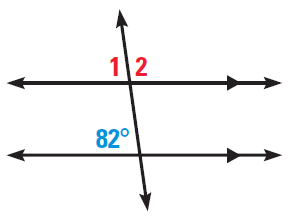
Click through the steps below to see how you can solve this problem and find the missing information.
| The Steps | How to Apply Each Step |
| Start with the given angle (82°). Decide how it is related to either angle 1 or angle 2. | The given angle (82°) is on the same side of the transversal line as angle 1, but it is inside the parallel lines while angle 1 is outside those lines. We could say that angle 1 and the given angle (82°) are corresponding angles because they are in corresponding positions in the diagram. |
| Decide which property can be used to find the missing information. Which property applies? |
We can use the property that corresponding angles formed from a transversal are congruent. Since its corresponding angle is 82°, we know that angle 1 is also 82°. |
| Decide how the known angle is related to the angle degree that is still missing. How is angle 1 related to angle 2? | Angle 1 and angle 2 together form a straight angle, an angle of 180°. That means that angle 1 and angle 2 are supplementary angles—together, they add up to 180°. |
| Do the math. If angle 1 is 82°, and it is supplementary to angle 2, what is the measure of angle 2? | m∠1 + m∠2 = 180°. If m∠1 = 82°, then m∠2 = 180° – 82° = 98°. Angle 2 is 98°. |
What is the value of variable x in the diagram below?
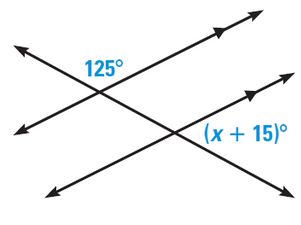
Click on the questions below to see how you can arrive at an answer.
| Question to Ask | How to Answer |
| How are the given angles (125° and (x+15)°) related to each other? | They are both on the outside of the parallel lines (exterior) and on the same side of the transversal (consecutive). The angles are consecutive exterior angles. |
| What angle property can I use to solve for x? | You can use the fact that consecutive exterior angles formed by a transversal are supplementary. |
| What equation should I set up to find the value of x? | 125 + (x + 15) = 180° x + 140 = 180° x = 180° – 140 = 40° |
