To do well in their jobs, architects, designers, and carpenters must be able to recognize the type of problem they have encountered and then remember how to solve it. If they paid close attention in their math classes, they could recognize a problem involving ratios and proportions fairly easily and then use a strategy like cross multiplication to solve the problem.
Before we look at more specific uses of ratios and proportions in various careers, let's review how to solve these types of problems. In your notebook, answer the question on each flash card. When you have written an answer, click the card to check your work.
Find x:
![]()
Use cross multiplication:
\(\small\mathsf{ \frac{5}{x} = \frac{2}{3} }\)
\(\small\mathsf{ 15 = 2x }\)
\(\small\mathsf{ x = 7.5 }\)
Find y:
![]()
Use cross multiplication:
\(\small\mathsf{ \frac{y}{4} = \frac{3}{2} }\)
\(\small\mathsf{ 2y = 12 }\)
\(\small\mathsf{ y = 6 }\)
The following two rectangles are similar. Find the missing side x:
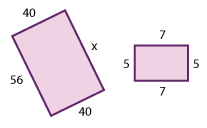
Since these two rectangles are similar, you can write the following proportion:
\(\small\mathsf{ \frac{40}{5} = \frac{x}{7} }\)
\(\small\mathsf{ 280 = 5x }\)
\(\small\mathsf{ x = 56 }\)
Cards remaining:
