The Golden Ratio is a specific ratio with an approximate value of 1.618. However, the Golden Ratio is really much more than just a number. It appears not only in geometry textbooks but also—quite frequently—in famous works of art and architecture, among other places. Click each image below to see the Golden Ratio in practice.
Golden Arm
The Golden Smile
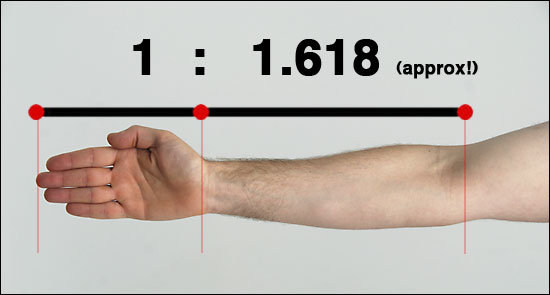
The Golden Ratio appears not only in art and architecture but also on our bodies. The ratio of a human's forearm to his or her hand is approximately 1.618.
Artists believe that using the Golden Ratio in paintings makes them more aesthetically pleasing. Each of the rectangles shown in the famous painting of Mona Lisa is drawn to the Golden Ratio, when you look at the ratio of length to width.
Watch this video to learn how to identify more examples of the Golden Ratio.
As you watch this video, use the study guide to follow along if you'd like. Click the button below to download the study guide.
Are some ratios more perfect than others? Well, it depends on who you ask. Some would say that certain geometric
dimensions are more pleasing to the eye than others. So, if the perfect height to width dimension can be found, than
that must represent the most perfect ratio.
The golden ratio, also known as the golden rectangle, golden section, golden number, golden proportion, divine
proportion, divine section, among others, has been identified as that most perfect ratio. Greek mathematicians and
artists observed the beauty of the Golden Ratio as early as 400 BC – more than two thousand years ago. The beautiful
and pleasing ratio of a measurement's height to width is observed in many objects. Whether the golden ratio was used
in the design of the objects is debatable, but the existence is not.
For example, the Golden Ratio is demonstrated in the Mona Lisa painting by Leonardo Da Vinci completed around the
year 1500. Several Golden Rectangles are shown here. The golden ratio is calculated by the proportion of the long side
length to the short side length of each rectangle. To assist in seeing the ratio, squares are added in each rectangle since
a square's width is equal to its height.
The Cathedral at Notre Dame also exhibits several golden rectangles. Examples in this front view range from the overall
height and width, to each of the three levels of construction, to the arches, and the doorways. Even Mother Nature
demonstrates the golden ratio. The intersections of the collapsing rectangles form a spiral seen in this nautilus shell.
And as described earlier in this module, the ratio of a person's hand to their forearm also displays the golden ratio. Even
the joints in one's fingers follow relatively close to the golden ratio. The smallest section of each finger compared to the
next also follows the golden ratio.
The last example I'll share with you is one from a polygon studied in geometry; a pentagon inset with a five-point star.
In this diagram the black and green segments are the same lengths. The ratio of the red to black or green segment is
represented by the golden number. The ratio of green or black to yellow, and the ratio of yellow to blue are
represented by the golden number. In fact, if I was to draw another five point star in the middle, you would continue to
see another series of segment lengths modelled by the golden number – a pattern that continues an infinite number of
times.
Having identified the golden ratio in so many circumstances, mathematicians in the seventeenth century began
searching for ways to define and calculate the number represented in the ratio. A definition for the ratio is shown here
and illustrated with the following diagram and equation. When the proportion of the length of a longer segment to
shorter segment is equal to the proportion of the total length to the longer segment, we observe the golden ratio.
Mathematically, the longer segment is always approximately 1.618 times the length of the short segment. Since this
number is so special, it has since been designated with its own Greek letter. Similar to how the Greek letter Pi represents
the ratio of a circles diameter to circumference, approximately 3.14159, the letter Phi ("fye"), sometimes pronounced
"fee" represents this ratio, the golden number approximately 1.618. More specifically though, the value of phi can be
found by calculating the quantity of one plus the square root of 5 divided by two.
For a proportion, or ratio, known for twenty-four hundred years, a simple five-minute video won't do it justice. For
further reading I recommend visiting the following websites. I also recommend checking out the video, Donald in
Mathemagic Land; a Walt Disney film released in 1959. The explanations and animations of the golden ratio are
excellent in that short film.
Question
How can you determine if the length to width ratio of a rectangle is "golden"?
Reduce the fraction by dividing the length of the rectangle by its width.
If the resulting ratio is approximately 1.618, then the rectangle represents the Golden Ratio.
