So far in this lesson, we have shown a conjecture to be true by providing specific examples and by making general statements that, taken together, prove the statement. These two approaches represent two different methods of proving conjectures: an informal proof and a formal proof. Use the tabs below to make sure you understand the difference between these two types of proofs.
Informal Proofs
Example
Formal Proofs
An informal proof uses several specific examples to show that something is true. While it is often easy to see that something is true using an informal proof, it is important to note that informal proofs do not prove that a conjecture is always true.
Suppose you were asked to prove this:
The sum of the exterior angles of a quadrilateral is 360 degrees.
An informal proof would list several specific angle measurements, showing that the sum of the exterior angles equals 360 degrees in each example.
| Quadrilateral #1 | Quadrilateral #2 | Quadrilateral #3 |
| Interior Angles A = 70 B = 95 C = 100 D = 95 |
Interior Angles A = 73 B = 92 C = 112 D = 83 |
Interior Angles A = 87 B = 91 C = 89 D = 93 |
| Exterior Angles 180 - A = 110 180 - B = 85 180 - C = 80 180 - D = 85 |
Exterior Angles 180 - A = 107 180 - B = 88 180 - C = 68 180 - D = 97 |
Exterior Angles 180 - A = 93 180 - B = 89 180 - C = 91 180 - D = 87 |
| Sum of Exterior Angles: 110 + 85 + 80 + 85 = 360 |
Sum of Exterior Angles: 107 + 88 + 68 + 97 = 360 |
Sum of Exterior Angles: 93 + 89 + 91 + 87 = 360 |
Now you try it. Provide several examples that show this conjecture is probably true.
The sum of two consecutive numbers is an odd number.
Write out some examples. Then click the button below to compare your list to ours.
Here's a possible list of examples. Yours may be a little different.
3 + 4 = 7 (odd)
10 + 11 = 21 (odd)
100 + 101 = 201 (odd)
-3 + -2 = -5 (odd)
-1 + 0 = -1 (odd)
Instead of a set of examples, a formal proof uses general statements and algebra or geometry rules and theorems to prove that a conjecture is always true.
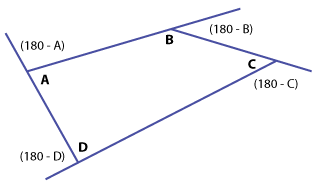
Suppose you were asked to provide formal proof for this same statement:

The sum of the exterior angles of a quadrilateral is 360 degrees.
A formal proof would use the general angles A, B, C, and D instead of listing several specific angles that support the statement. The formal proof would look like this:
The sum of A + B + C + D = 360, because the sum of the interior angles of a quadrilateral is 360 degrees.
The sum of the exterior angles is
(180 - A) + (180 - B) + (180 - C) + (180 - D) = 4 · 180 - (A + B + C + D).
720 - 360 = 360.
This equation shows that the conjecture is true no matter what the values of A, B, C, and D are.
Question
What is the difference between an informal and formal proof?
