Now see if you can make a conjecture about a topic. Similar triangles have congruent corresponding angles, and their corresponding sides have the same ratio, but are not equal in length. Look closely at these two similar triangles.
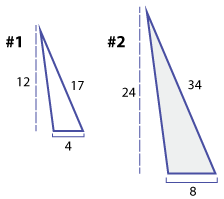
What do you think is true about the ratio of the areas of these two triangles?
You may have said that the area of the larger triangle is twice the area of the smaller triangle, especially if you noticed that the lengths of the corresponding sides are doubled. To describe these two triangles, you could say that the similarity ratio is 1:2 or \(\mathsf{ \frac{1}{2} }\). However, since you're looking for the ratio of areas, you would need to calculate the areas of the two triangles.
The ratio of the area of triangle #1 to triangle #2 is \(\mathsf{ \frac{24}{96} }\), or \(\mathsf{ \frac{1}{4} }\)—not \(\mathsf{ \frac{1}{2} }\).
| Area of Triangle #1 | Area of Triangle #2 |
| \(\mathsf{ A = \frac{1}{2} \cdot 12 \cdot 4 }\) \(\mathsf{ A = 24 }\) |
\(\mathsf{ A = \frac{1}{2} \cdot 24 \cdot 8 }\) \(\mathsf{ A = 96 }\) |
Question
What do you notice about the relationship between the similarity ratio of the two triangles (\(\mathsf{ \frac{1}{2} }\)) and the ratio of the areas (\(\mathsf{ \frac{1}{4} }\))? Make a conjecture that describes this relationship.
One reason this statement is a good conjecture is that it is likely true. After all, we just saw an example that demonstrates its "truth." However, we still haven't proved the conjecture—the rules of logic are required for formal proofs.
