Video: Adding and Subtracting Fractions with Unlike Denominators
Watch the video for an introduction to adding and subtracting fractions with unlike denominators.
Goal:
Goal:
|
Scene # |
Description |
Narration |
|
1 |
A man is standing by a car with a tire removed. On the freeway sign above his head fractions appear that he is talking about. The camera zooms in on the sign and as the man talks the math problems he talks about appear on the screen. |
- YOU'RE READY TO ADD AND SUBTRACT FRACTIONS WITH DENOMINATORS THAT ARE NOT THE SAME. NOW, FIRST WE FIND THE LOWEST COMMON DENOMINATOR. HERE'S HOW WE DO THAT. WE LOOK AT THE DENOMINATORS OF THE FRACTIONS. WE ASK, "WHAT'S THE FIRST COMMON NUMBER FOR THE DENOMINATORS?" WHAT IS THE FIRST COMMON NUMBER FOR 6 AND 4? IT'S 12. IT'S THE FIRST COMMON NUMBER, SO IT'S THE LOWEST COMMON DENOMINATOR. WE WRITE THE LOWEST COMMON DENOMINATOR FOR BOTH FRACTIONS. NOW WE FIND THE EQUIVALENT FRACTIONS FOR 1/4 AND 4/6. FIRST, WE FIGURE OUT THE FRACTIONS OF 1 IN BOTH EQUATIONS. HERE, WE MULTIPLY 4 BY 3 TO GET 12. SO THE FRACTION OF 1 IS 3/3. WE MULTIPLY 6 BY 2 TO GET 12, SO THE FRACTION OF 1 IS 2/2. NOW WE COMPLETE THE 2 EQUATIONS. FIRST THE TOP EQUATION, THEN THE BOTTOM EQUATION. NOW WE ADD THE FRACTIONS. |
|
2 |
A cartoon character with orange hair appears in the top left corner of a pink screen. A fraction problem is on the screen. As the narrator speaks the numbers, fractions and problems appear on the screen. |
- HERE'S 4 MINUS 2/5. YOU KNOW HOW TO WORK PROBLEMS WITH A WHOLE NUMBER AND A FRACTION. YOU CAN WORK THE PROBLEM THE SAME WAY WHEN IT'S WRITTEN LIKE THIS. FIRST, WE WRITE 4 AS A SIMPLE FRACTION. WHAT FRACTION? - YES, 4 OVER 1. CAN WE SUBTRACT THE WAY THE FRACTIONS ARE WRITTEN? - RIGHT, WE CAN'T. SO WE FIND THE LOWEST COMMON DENOMINATOR. WE JUST CHANGED 4 INTO A FRACTION THAT HAS THE SAME DENOMINATOR AS THE OTHER FRACTION. WHAT DENOMINATOR IS THAT? YES, 5. WE WRITE THE FRACTION 2/5 HERE. THEN WE CHANGE 4 INTO A FRACTION THAT HAS A DENOMINATOR OF 5. WHAT FRACTION IS THAT? - YES, 20/5. NOW WE COPY THE SIGN AND SUBTRACT. REMEMBER, WE'RE DOING THE SAME THING WE'VE ALWAYS DONE WITH A FRACTION AND A WHOLE NUMBER. WE'RE MAKING THE DENOMINATORS THE SAME. LET'S WORK THIS PROBLEM. FIRST WE WRITE 8 AS A FRACTION. BOTH FRACTIONS MUST HAVE THE SAME DENOMINATOR. WHAT DENOMINATOR? YES, 4. WE COPY THE FRACTION 3/4 HERE. NOW WE WRITE THE WHOLE NUMBER AS A FRACTION THAT EQUALS 8 AND HAS A DENOMINATOR OF 4. WHAT'S THE FRACTION? - YES, 32/4. WE COPY THE SIGN AND ADD. |
|
3 |
A woman is standing by a car on a street. A billboard has a fraction displayed on it. The problem the woman describes appears on the billboard as she walks through the steps. |
REMEMBER, WHEN YOU ADD OR SUBTRACT A WHOLE NUMBER AND A FRACTION, YOU CAN WORK THE PROBLEM THIS WAY OR THIS WAY. YOU MAKE THE DENOMINATORS THE SAME AND THEN WORK THE PROBLEM. AND YOU GET THE SAME ANSWER IF YOU WRITE THE FRACTION OF 1 FOR THE WHOLE NUMBER. THE FRACTION OF 1 JUST SHOWS WHAT YOU MULTIPLIED 4 BY TO GET 20/5. |
|
4 |
A man walks on a street towards a bus stop. On the wall of the building by the bus stop more fraction problems appear. |
- HERE ARE SOME COMMON DENOMINATOR PROBLEMS. THEY ARE EASIER TO WORK WHEN THEY ARE WRITTEN LIKE THIS. SO WHEN YOU ARE GIVEN A PROBLEM LIKE THIS, CHECK THE SIGN TO MAKE SURE IT'S A COMMON DENOMINATOR PROBLEM. THEN REWRITE IT LIKE THIS. IF IT IS A MULTIPLICATION PROBLEM, WORK IT THE WAY IT IS WRITTEN. |
You saw a few examples in the video lesson. Let's look at a few more.
Example 1: 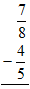
| Find the LCD: | the LCD of 5 and 8 is 40 | ||
| Make equivalent fractions so that the fractions have a common denominator |
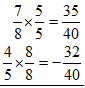 |
||
| Add or subtract: | 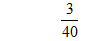 |
||
| Reduce if possible: | 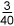 is already in lowest terms. is already in lowest terms. |