Practice Performing a Positive Rotation

Let's Review

You have learned that you can rotate an object \(90^\circ\) around the ordered pair \(\left(0,0\right)\) using the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\). While you can rotate any object any number of positive degrees around a center of rotation, the more common degrees of rotation are \(90^\circ, 180^\circ,\) and \(270^\circ\). Each of these has its own transformation.

Transformations for Rotations of \(90^\circ,180^\circ,270^\circ,\) and \(360^\circ\)

\(R_{90^\circ}:\left(x,y\right)\rightarrow\left(-y,x\right)\)

\(R_{180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\)

\(R_{270^\circ}:\left(x,y\right)\rightarrow\left(y,-x\right)\)

\(R_{360^\circ}:\left(x,y\right)\rightarrow\left(x,y\right)\)

Let's Practice

Use your knowledge of rotations in the coordinate plane to complete the activity below. Answer the question on each tab, then check your answer.

Suppose that PizzaBee can simultaneously bake multiple pizzas on the spinners in their oven. Two pizzas that are in one oven are represented on the coordinate plane below.

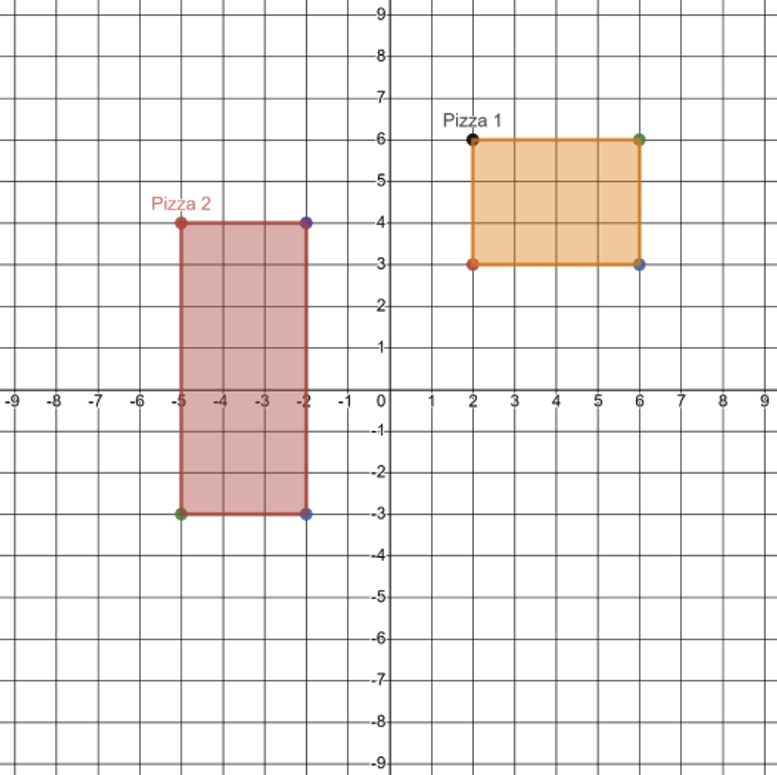
A detailed description of this image follows in the next paragraph.

Give the coordinates of the vertices of the image of Pizza 1 after a 180° rotation \( (R_{180^{\circ}}) \) around the origin.

After a \(180^\circ\) rotation about the origin, the vertices will be

\(\left(-2,-3\right)\)

\(\left(-2,-6\right)\)

\(\left(-6,-3\right)\)

\(\left(-6,-6\right)\)

If you need help arriving at this answer, click the Solution button.

Understand the problem.	You are asked to rotate the vertices of Pizza 1 by \(180^\circ\) around the origin. This will rotate Pizza 1 counterclockwise.
Name the vertices of the preimage.	The vertices of the preimage are \(\left(2,3\right)\) \(\left(2,6\right)\) \(\left(6,3\right)\) \(\left(6,6\right)\)
Apply the transformation \(R_{180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\).	\(\left(2,3\right)\rightarrow\left(-2,-3\right)\) \(\left(2,6\right)\rightarrow\left(-2,-6\right)\) \(\left(6,3\right)\rightarrow\left(-6,-3\right)\) \(\left(6,6\right)\rightarrow\left(-6,-6\right)\)
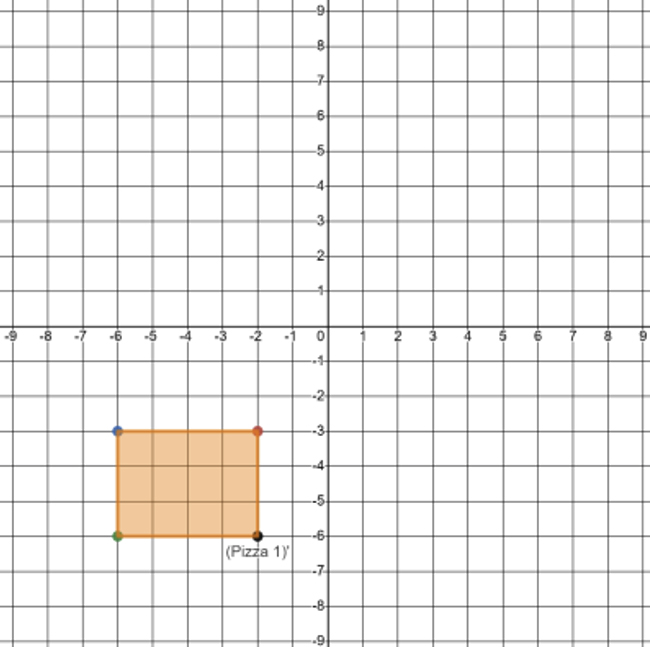
Here is a graph of the image. Notice that the rotation moved the preimage from quadrant 1 to quadrant 3.	A quadrilateral drawn on a coordinate plane representing (Pizza 1)′ and its coordinates are (negative 2,negative 3), (negative 2,negative 6), (negative 6, negative 3), and (negative 6, negative 6).

Suppose that PizzaBee can simultaneously bake multiple pizzas on the spinners in their oven. Two pizzas that are in one oven are represented on the coordinate plane below.

Give the coordinates of the vertices of the image of Pizza 2 after a rotation of \(270^\circ\left(R_{270^\circ}\right)\) around the origin.

After a \(270^\circ\) rotation about the origin, the vertices will be

\(\left(-5,4\right)\rightarrow\left(4,5\right)\)

\(\left(-5,-3\right)\rightarrow\left(-3,5\right)\)

\(\left(-2,4\right)\rightarrow\left(4,2\right)\)

\(\left(-2,-3\right)\rightarrow\left(-3,2\right)\)

If you need help arriving at this answer, click the Solution button.

Understand the problem.	You are asked to rotate the vertices of Pizza 2 by \(270^\circ\) around the origin. This will rotate Pizza 2 counterclockwise.
Name the vertices of the preimage.	The vertices of the preimage are \(\left(-5,4\right)\) \(\left(-5,-3\right)\) \(\left(-2,4\right)\) \(\left(-2,-3\right)\)
Apply the transformation \(R_{270^\circ}:\left(x,y\right)\rightarrow\left(y,-x\right)\).	\(\left(-5,4\right)\rightarrow\left(4,5\right)\) \(\left(-5,-3\right)\rightarrow\left(-3,5\right)\) \(\left(-2,4\right)\rightarrow\left(4,2\right)\) \(\left(-2,-3\right)\rightarrow\left(-3,2\right)\)
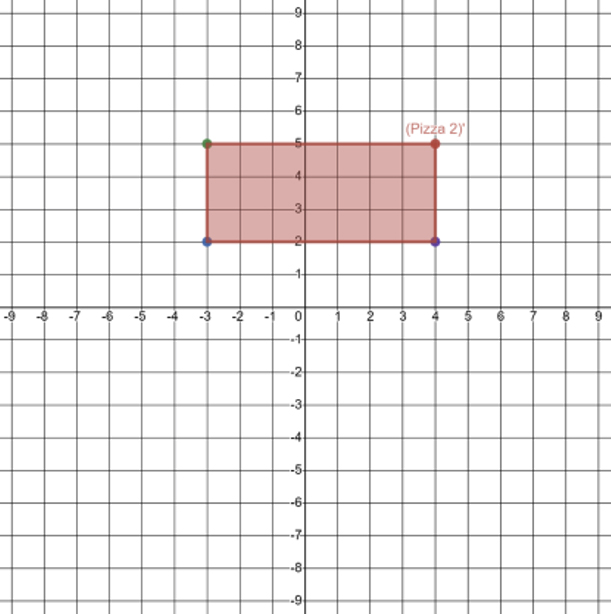
Here is a graph of the image.	A quadrilateral drawn on a coordinate plane representing (Pizza 2)′ and its coordinates are (negative 3, 2), (negative 3, 5), (4, 2), and (4, 5).

Look at the line segment below.

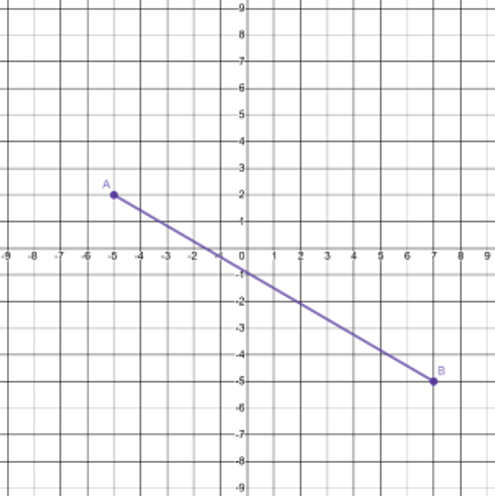
A line segment drawn on the coordinate plane with coordinates A(negative 5, 2) and B(7, negative 5).

Look at the graphs below. Click the graph that shows the image of this line segment after a rotation of \(90^\circ\) \(\left(R_{90^\circ}\right)\).

Not Quite!

Remember that the transformation for a positive \(90^\circ\) rotation is \(R_{90^\circ}:\left(x,y\right)\rightarrow\left(-y,x\right)\). Find the coordinates of the endpoints of the line segment and then apply that transformation.

Yes!

The transformation for a positive \(90^\circ\) rotation is \(R_{90^\circ}:\left(x,y\right)\rightarrow\left(-y,x\right)\). This means that \(A\left(-5,2\right)\rightarrow A^\prime\left(-2,-5\right)\) and \(B\left(7,-5\right)\rightarrow\left(5,7\right)\).

Not Quite!

Remember that the transformation for a positive \(90^\circ\) rotation is \(R_{90°}:\left(x,y\right)\rightarrow\left(-y,x\right)\). Find the coordinates of the endpoints of the line segment and then apply that transformation.

Text

Guided Notes

Tutor

Video

How To

Meet your new study partner! With our powerful Student Tools, your online learning experience just got more accessible, personalized, and thought-provoking than ever before!

Do you feel like you learn better when you watch videos? You’re not alone! Research shows instructional videos can make learners more engaged and active in online classes, when compared to text-only lessons.

Student Tools lets you turn some lesson pages into videos instantly! Just click the Student Tools tab and select Video. Remember, video instruction is not available on every lesson page.