Loading...

How well do you understand the concepts and skills introduced in this lesson?

Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each answer is correct—if you do not, review that part of the lesson.

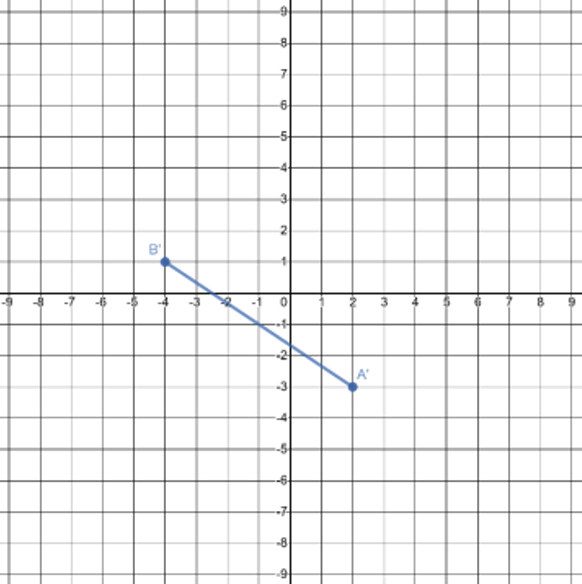
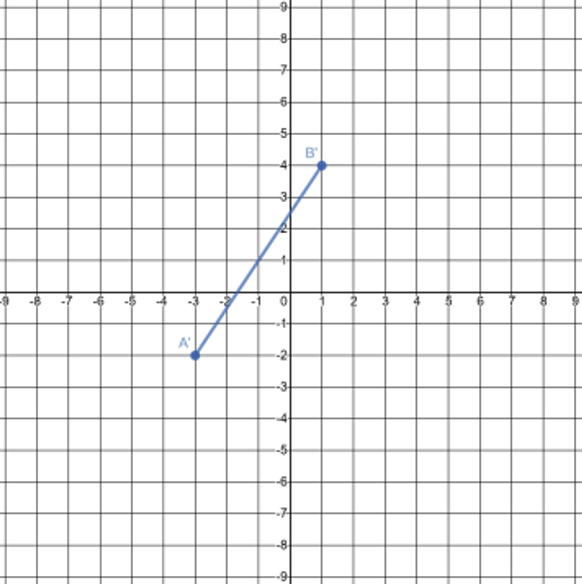
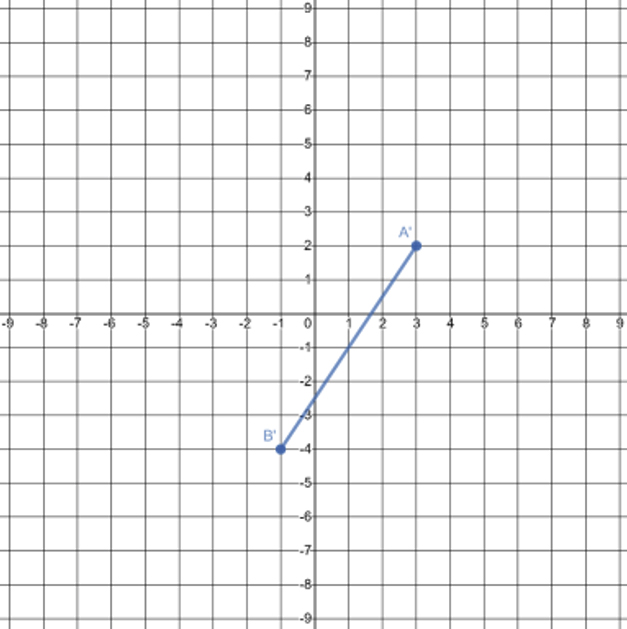
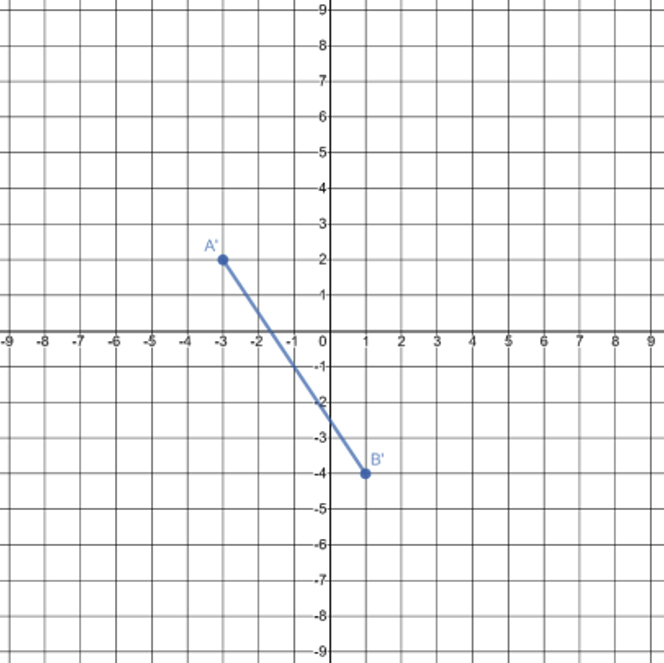
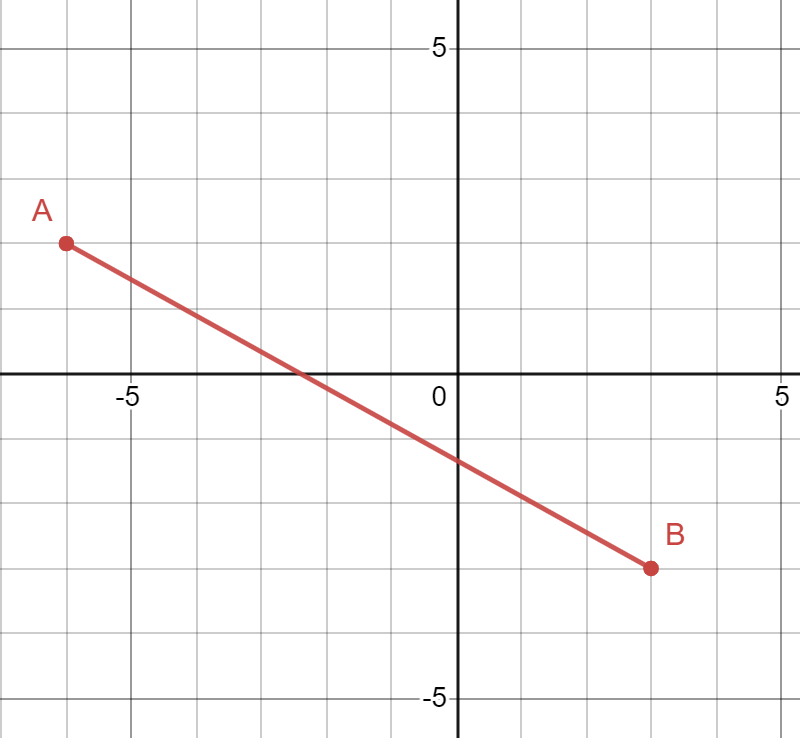
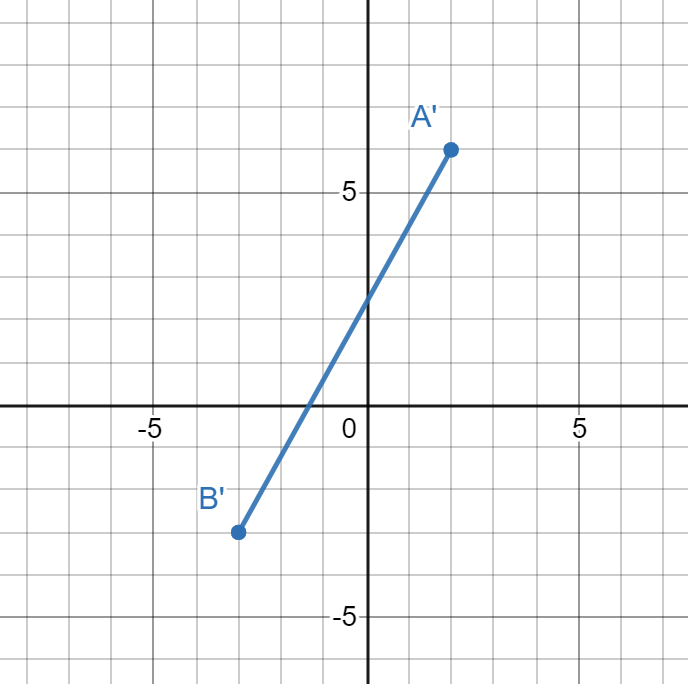
Which graph is of the image of \(\overline{\text{AB}}\) after \(R_{90^\circ}\) around the origin?

A line segment drawn on the coordinate plane with coordinates A(negative 2, 3) and B(4, negative 1).

  1. A line segment drawn on the coordinate plane with coordinates A′(2, negative 3) and B′(negative 4, 1).
  2. A line segment drawn on the coordinate plane with coordinates A′(3, 2) and B′(negative 1, negative 4).
  3. A line segment drawn on the coordinate plane with coordinates A′(negative 3, 2) and B′(1, negative 4)

To perform the rotation \(R_{90^\circ}\) with the origin as the center of rotation, use the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

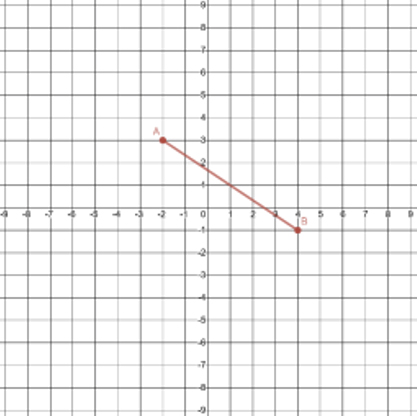
To perform the rotation \(R_{90^\circ}\) with the origin as the center of rotation, use the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\). This means that \(\text{A}\left(-2,3\right)\rightarrow \text{A}^\prime\left(-3,-2\right)\) and \(\text{B}\left(4,-1\right)\rightarrow\left(1,4\right)\) as shown in this graph.

To perform the rotation \(R_{90^\circ}\) with the origin as the center of rotation, use the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

To perform the rotation \(R_{90^\circ}\) with the origin as the center of rotation, use the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

Suppose the preimage of point \(\text{P}\) is located at \(\left(-23,45\right)\). If \(\text{P}\) is rotated \(180^\circ\) clockwise around the origin, in what quadrant can you find its image?

  1. Quadrant 1

  2. Quadrant 2

  3. Quadrant 3

A rotation \(180^\circ\) clockwise around the origin means \(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\). In what quadrant would you find \(\text{P}\left(-23,45\right)\rightarrow \text{P}^\prime\left(23,-45\right)\)?

A rotation \(180^\circ\) clockwise around the origin means \(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\). In what quadrant would you find \(\text{P}\left(-23,45\right)\rightarrow \text{P}^\prime\left(23,-45\right)\)?

A rotation \(180^\circ\) clockwise around the origin means \(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\). In what quadrant would you find \(\text{P}\left(-23,45\right)\rightarrow \text{P}^\prime\left(23,-45\right)\)?

A rotation \(180^\circ\) clockwise around the origin means \(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\). The transformation is \(\text{P}\left(-23,45\right)\rightarrow \text{P}'\left(23,-45\right)\). Since the \(x\)-coordinate is positive and the \(y\)-coordinate is negative, you can find \(\text{P}^\prime\) in quadrant 4.

Determine the rotation around the origin that was performed to transform the preimage on the left to its image on the right.

Preimage

Image
A line segment drawn on the coordinate plane with coordinates A(negative 6, 2) and B(3, negative 3). Use enter key to open full-screen view.
A line segment drawn on the coordinate plane with coordinates A(negative 6, 2) and B(3, negative 3). Use escape key to exit full-screen view.
A line segment drawn on the coordinate plane with coordinates A′(2, 6) and B′(negative 3, negative 3). Use enter key to open full-screen view.
A line segment drawn on the coordinate plane with coordinates A′(2, 6) and B′(negative 3, negative 3). Use escape key to exit full-screen view.

  1. \(R_{-270^\circ}\)

  2. \(R_{90^\circ}\)

  3. \(R_{-180^\circ}\)

State the coordinates of the endpoints of the two line segments. Since \(\text{A}\left(-6,2\right)\rightarrow \text{A}^\prime\left(2,6\right)\) and \(\text{B}\left(3,-3\right)\rightarrow \text{B}^\prime\left(-3,-3\right)\), the rotation is \(R_{270^\circ}\).

Look at how the corresponding coordinates change from the line segment \(\text{AB}\) to the line segment \(\text{A}^\prime \text{B}^\prime\). The relationship is \(\left(x,y\right)\rightarrow\left(y,-x\right)\). Which rotation has this relationship?

Look at how the corresponding coordinates change from the line segment \(\text{AB}\) to the line segment \(\text{A}^\prime\text{B}^\prime\). The relationship is \(\left(x,y\right)\rightarrow\left(y,-x\right)\). Which rotation has this relationship?

Look at how the corresponding coordinates change from the line segment \(\text{AB}\) to the line segment \(\text{A}^\prime\text{B}^\prime\). The relationship is \(\left(x,y\right)\rightarrow\left(y,-x\right)\). Which rotation has this relationship?

Give the coordinates of the image of point \(\text{P}\) after a rotation of \(-270^\circ\) around the origin if its preimage is located at \(\left(1,-3\right)\).

  1. \(\left(-1,3\right)\)

  2. \(\left(-3,-1\right)\)

  3. \(\left(3,-1\right)\)

A clockwise rotation of \(270^\circ\) results in the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

A clockwise rotation of \(270^\circ\) results in the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\), so \(\text{P}\left(1,-3\right)\rightarrow \text{P}^\prime\left(3,1\right)\).

A clockwise rotation of \(270^\circ\) results in the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

A clockwise rotation of \(270^\circ\) results in the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).

Which notation would result in a counterclockwise rotation?

  1. \(R_{-270^\circ}\)

  2. \(R_{-90^\circ}\)

  3. \(R_{-180^\circ}\)

Counterclockwise rotations are positive.

Counterclockwise rotations are positive.

Counterclockwise rotations are positive.

This notation indicates a rotation of \(+180^\circ\), so it is counterclockwise.

Suppose there are two objects in the coordinate plane. One object is a preimage, and the other is its rotated image. The center of rotation is the origin.

Are these two objects congruent? Explain.

  1. Yes, a preimage and its rotated image are congruent only when the center of rotation is \(\left(0,0\right)\).

  2. No, rotation is not a rigid motion, and so a rotated image is not congruent with its preimage.

  3. No, rotation does not create a preimage and an image.

Since rotation is a rigid motion, an object's image will always be congruent with its preimage.

Rotation creates congruent objects in the coordinate plane regardless of the center of rotation.

Rotation is a rigid motion and so an object's image will always be congruent to its preimage.

Rotation is a transformation. Performing a rotation creates an image for the preimage.

Summary

Questions answered correctly:

Questions answered incorrectly: