To rotate an object in the coordinate plane, you need to know the center of rotation, the degree of rotation, and the direction rotation. You can find most of this information from the notation \(R_{degrees}\). But how do you use this information to actually perform a rotation? Read through the example below to find out.
The ordered pairs on the coordinate plane below represent a pizza that is baking in one of PizzaBee’s special ovens.
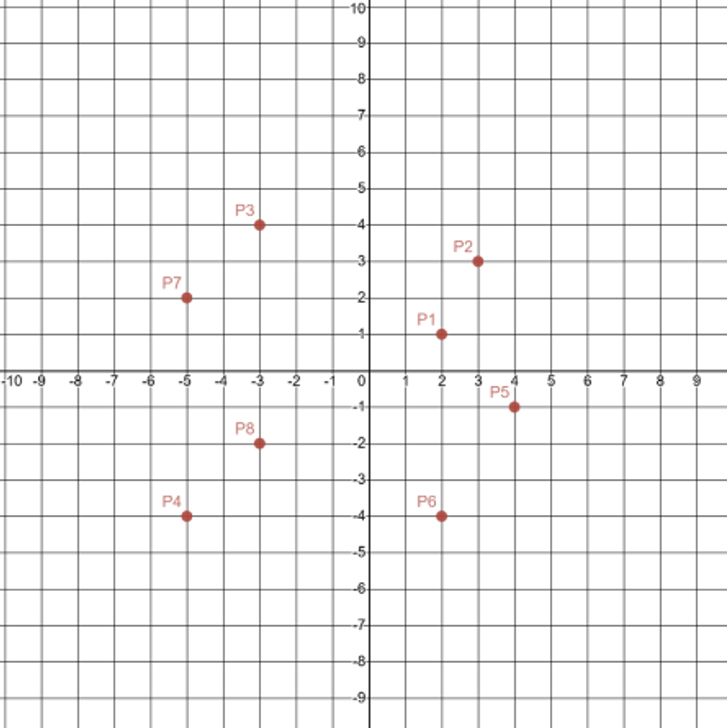
A coordinate plane with the following orders pairs plotted: P1(2, 1), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(negative 5, 2), P8(negative 3, negative 2).
Perform a rotation of \(R_{90^\circ}\) on the points \(\text{P}1\) and \(\text{P}8\) using \(\left(0, 0\right)\) as the center of rotation.
|
Understand the problem. |
You are asked to rotate the points \(\text{P}1\) and \(\text{P}8\) by positive \(90^\circ\). This means the points will rotate counterclockwise. The center of rotation is \(\left(0,0\right)\). |
|
Visualize how the point will rotate by sketching a triangle to connect the center of rotation \(\left(0, 0\right)\) to \(\text{P}1\left(2,1\right)\). |
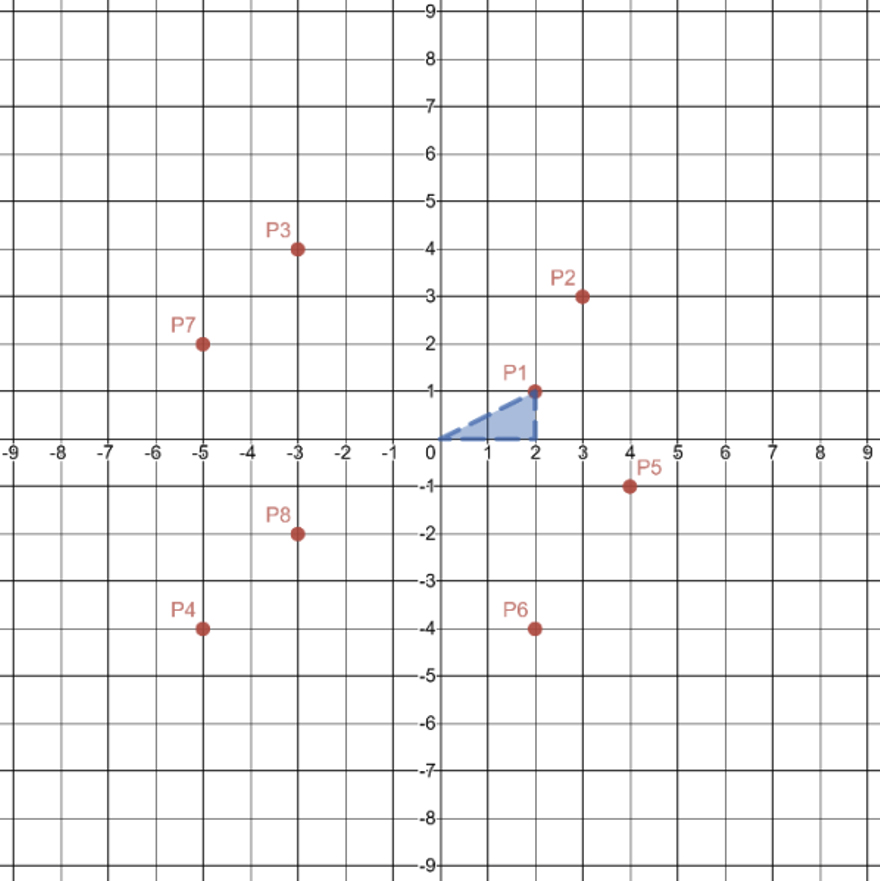
A coordinate plane with the following orders pairs plotted: P1(2, 1), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(-5, 2), P8(negative 3, negative 2). A right triangle is drawn using (0,0), P1 and the x-axis. |
|
Rotate the triangle \(90^\circ\) counterclockwise around the origin. After the \(90^\circ\) rotation, \(\text{P}1\left(2,1\right)\rightarrow\text{P}1^\prime\left(-1,2\right).\) |
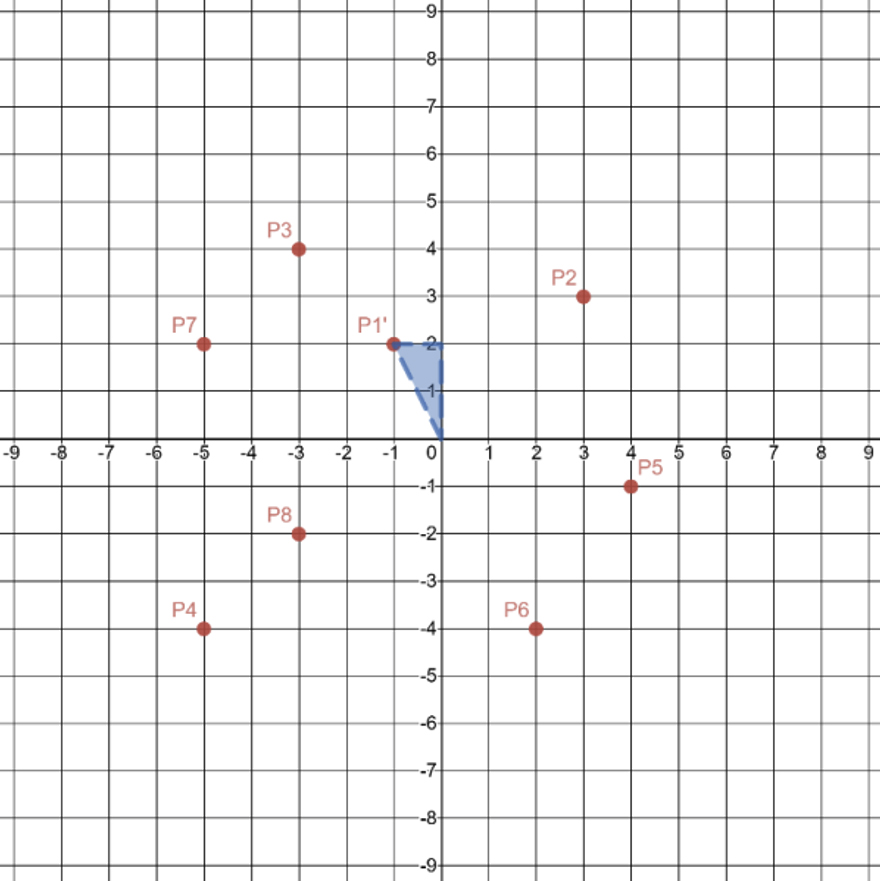
A coordinate plane with the following orders pairs plotted: P1′(negative 1, 2), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(negative 5, 2), P8(negative 3, negative 2). A right triangle is drawn using (0, 0), P1′ and the y-axis. |
|
Carry out the same process for the point \(\text{P}8\) by connecting it to the center of rotation. |
Create the triangle. 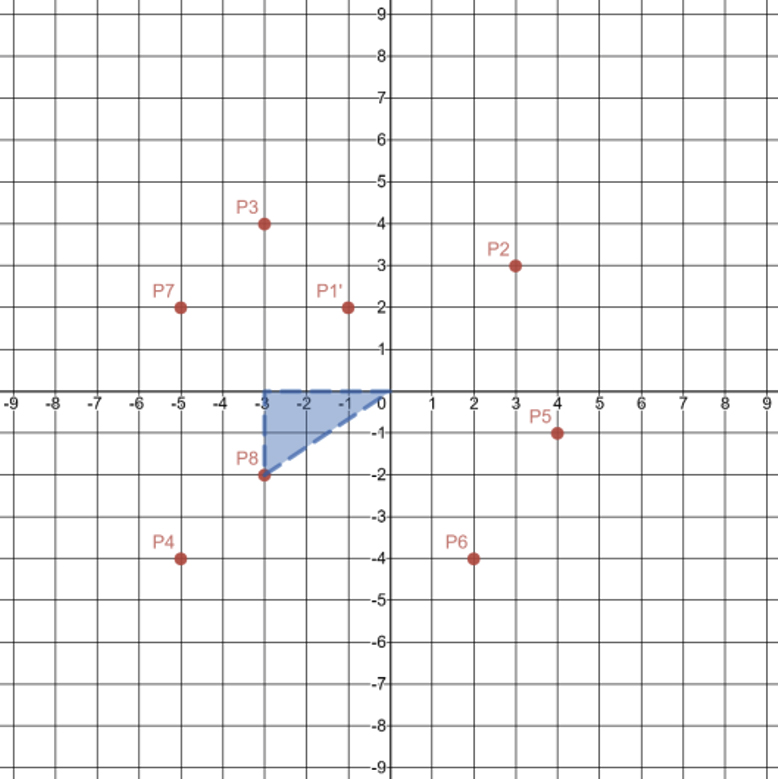
A coordinate plane with the following orders pairs plotted: P1′(2, 1), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(negative 5, 2), P8(negative 3, negative 2). A right triangle is drawn using (0, 0), P8 and the x-axis. |
|
Rotate the triangle \(90^\circ\) counterclockwise around the origin. After the \(90^\circ\) rotation, \(\text{P}8\left(-3,-2\right)\rightarrow\left(2,-3\right).\) |
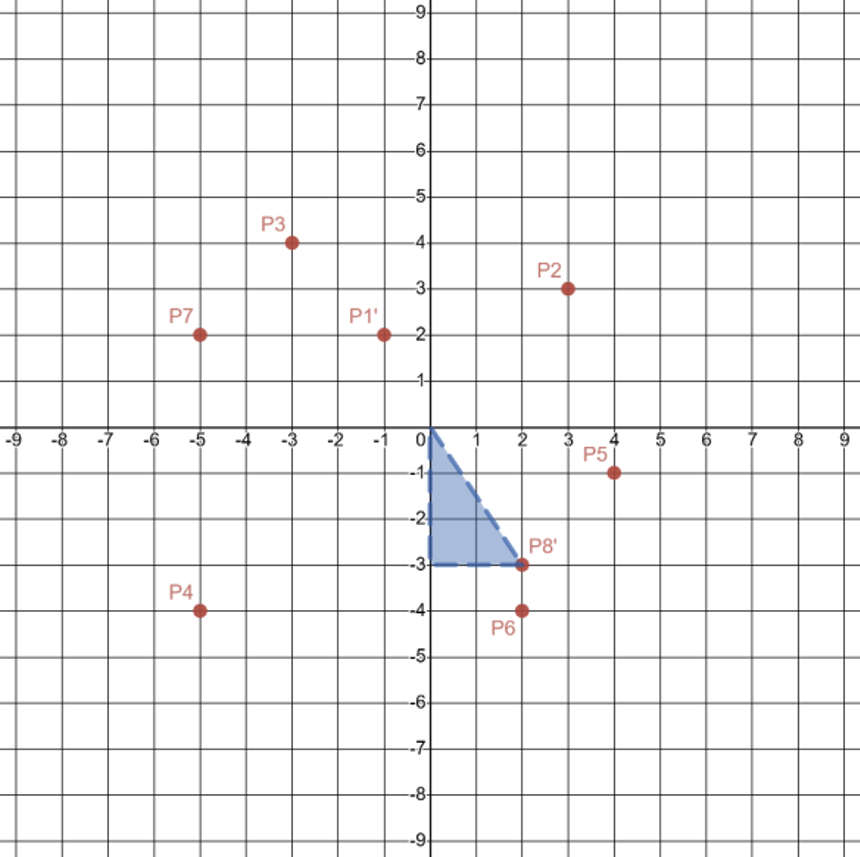
A coordinate plane with the following orders pairs plotted: P1′(2, 1), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(negative 5, 2), P8′(2, negative 3). A right triangle is drawn using (0, 0), P8 and the y-axis. |
In the example above, the point \(\text{P}1\) transformed from \(\left(2,1\right)\) to \(\left(-1,2\right)\), and the point \(\text{P}8\) transformed from \(\left(-3,-2\right)\) to \(\left(2,-3\right)\). When rotating a point or any object in the plane by positive \(90^\circ\), the transformation is \(\left(x,y\right)\rightarrow\left(-y,x\right)\).
Question
Use what you have learned to perform a rotation of \(R_{90^\circ}\) on the points \(\text{P}2\) through \(\text{P}7\) using \(\left(0,0\right)\) as the center of rotation.
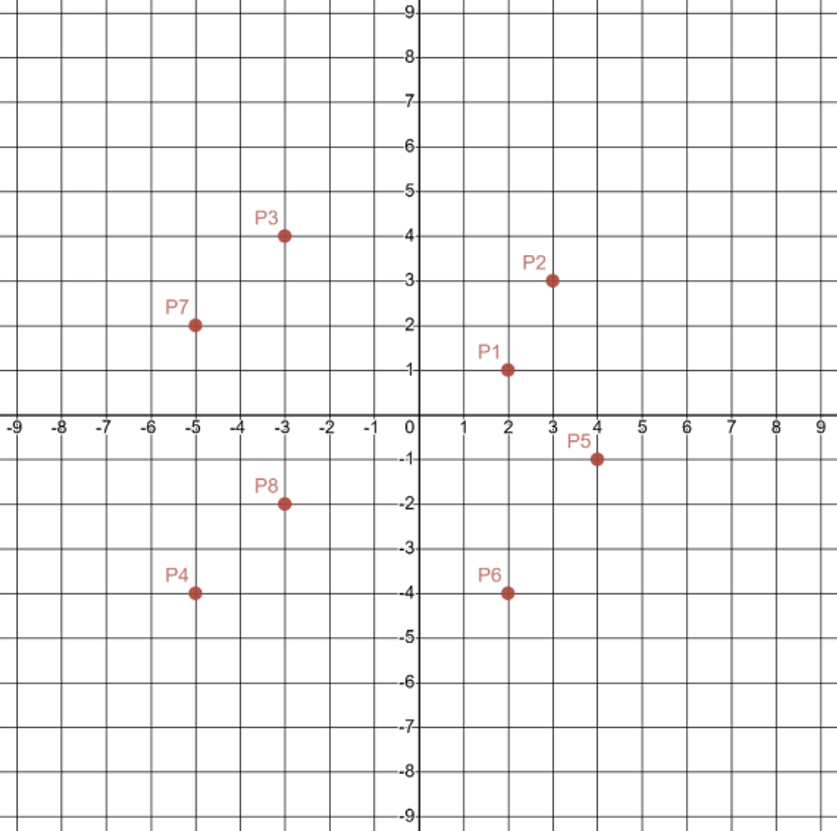
A coordinate plane with the following orders pairs plotted: P1(2, 1), P2(3, 3), P3(negative 3, 4), P4(negative 5, negative 4), P5(4, negative 1), P6(2, negative 4), P7(negative 5, 2), P8(negative 3, negative 2).
Since you are rotating all the points by positive \(90^\circ\), you can identify the ordered pairs that represent points \(\text{P}2\) through \(\text{P}7\) and then use the transformation \(\left(x,y\right)\rightarrow\left(-y,x\right)\).
\(\text{P}2\left(3,3\right)\rightarrow\text{P}2^\prime\left(-3,3\right)\)
\(\text{P}3\left(-3,4\right)\rightarrow\text{P}3^\prime\left(-4,-3\right)\)
\(\text{P}4\left(-5,-4\right)\rightarrow\text{P}4^\prime\left(4,-5\right)\)
\(\text{P}5\left(4,-1\right)\rightarrow\text{P}5^\prime\left(1,4\right)\)
\(\text{P}6\left(2,-4\right)\rightarrow\text{P}6^\prime\left(4,2\right)\)
\(\text{P}7\left(-5,2\right)\rightarrow\text{P}7^\prime\left(-2,-5\right)\)
