Aeryn is the owner of a pizzeria called PizzaBee.
She designed a pizza oven that has a special spinner inside.
When it is time to bake a pizza, a PizzaBee employee places it on the spinner.
The spinner slowly rotates the pizza in the oven. This helps ensure that the pizza bakes evenly.
The oven spinner works like this:
Suppose the coordinate plane represents the location of pepperoni slices on the pizza.
Each of P-sub 1 through P-sub 8 is an individual slice of pepperoni.
As the spinner rotates the pizza, the locations of the pepperoni slices change.
If the pizza rotates 90 degrees, then the pepperoni will also rotate 90 degrees.
Rotation is a mathematical term that describes the circular movement of an object on the coordinate plane around a fixed point.
Like translation and reflection, rotation is a rigid motion.
Rigid motion is a movement that does not change the size or shape of an object.
As the pizza rotates, the location of the toppings changes, but they do not change their size or shape.
In this lesson, you will learn how to rotate shapes in the coordinate plane.
You will also learn how to show that the resulting figure of a rotation is congruent to the original figure.
Question
In the video, you saw the preimage and image of points that had been rotated \(90^\circ\) in the coordinate plane. These images are repeated below.
| Preimage | Image |
|---|---|

A coordinate plane with the following orders pairs plotted: P1(2,1), P2(3,3), P3(negative3,4), P4(negative5, negative4), P5(4,negative1), P6(2, negative4), P7(negative5, 2), P8(negative3,negative2). |
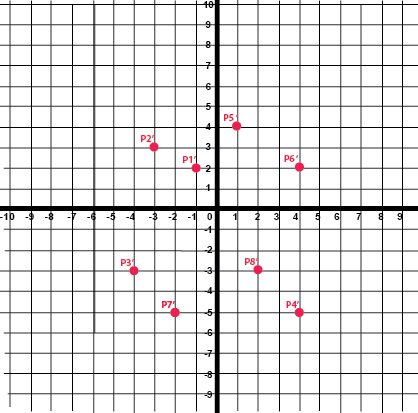
A coordinate plane with the following orders pairs plotted: P1′(-1,2), P2′(3,-3), P3′(-4,-3), P4′(4,-5), P5′(1,4), P6′(4,2), P7′(-2,-5), P8′(2,-3). |
What do you notice about the quadrant locations of the points in the image compared to the preimage?
The image of each point is located in a different quadrant than its preimage.
