The video you watched showed you how to rotate objects clockwise in the coordinate plane. This type of transformation is negative and spins objects to the right. The transformations for common degrees of clockwise, or negative, rotation are shown.
Transformations for Rotations of \(-90^\circ,-180^\circ,-270^\circ\) and \(360^\circ\)
\(R_{-90^\circ}:\left(x,y\right)\rightarrow\left(y,-x\right)\)
\(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\)
\(R_{-270^\circ}:\left(x,y\right)\rightarrow\left(-y,x\right)\)
\(R_{-360^\circ}:\left(x,y\right)\rightarrow\left(x,y\right)\)
How well can you rotate objects in the coordinate plane in a clockwise direction? Use the activity below to practice. Answer the question on each tab, then check your answer.
Some of the questions will ask you to create a graph.
If you need graph paper, click below to download printable graph paper in Word or PDF format.
Perform a rotation of \(R_{-90^\circ}\) on \(\triangle\text{ABC}\). Use the origin as the center of rotation.
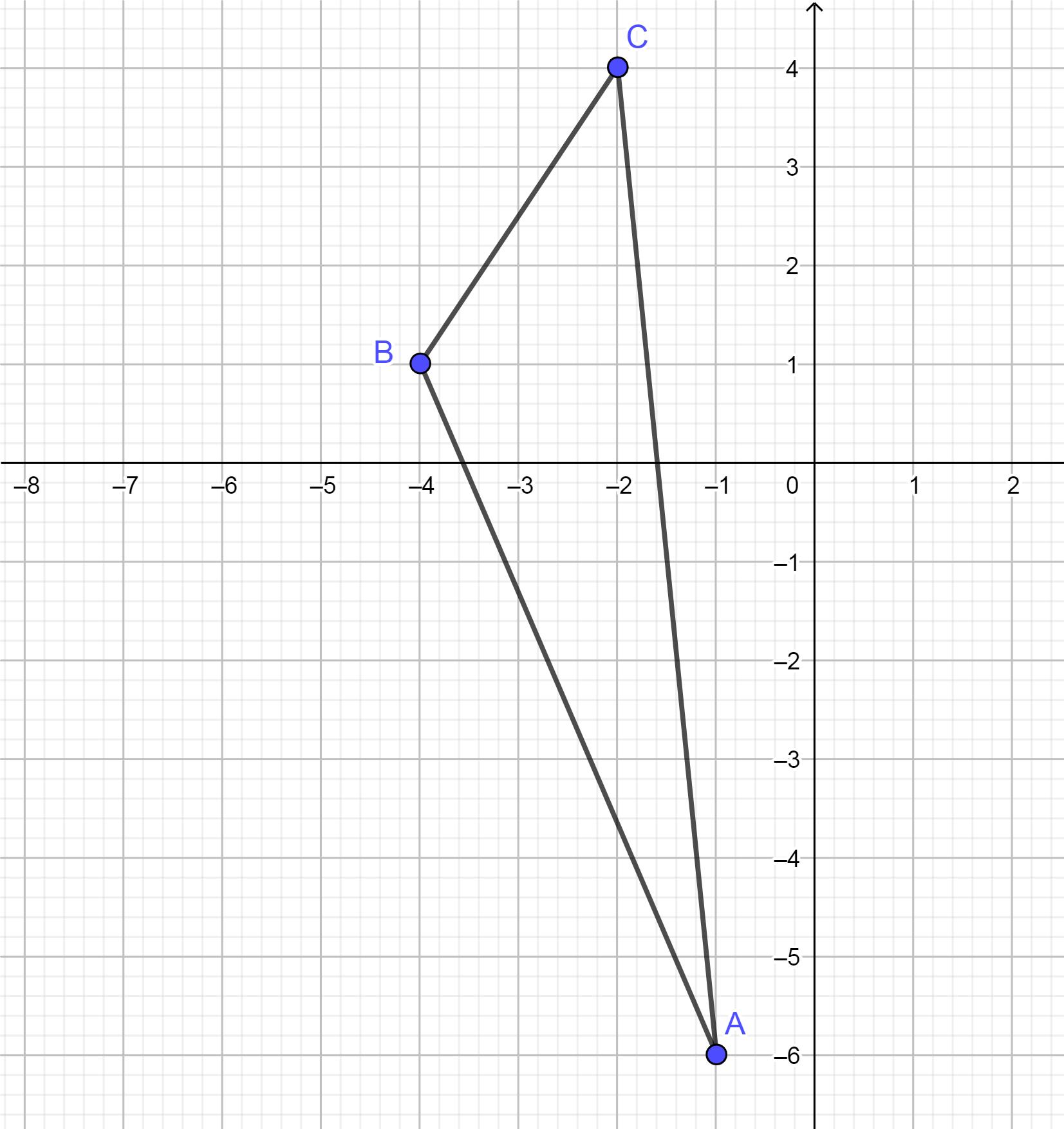
If you need help arriving at this answer, click the Solution button.
Understand the problem. |
You are asked to rotate the triangle \(90^\circ\) clockwise. The center of rotation is \(\left(0,0\right)\). |
Name the vertices of the preimage. |
The vertices of the preimage are \(\text{A}\left(-1,-6\right)\) \(\text{B}\left(-4,1\right)\) \(\text{C}\left(-2,4\right)\) |
Apply the transformation \(R_{-90^\circ}:\left(x,y\right)\rightarrow\left(y,-x\right).\) |
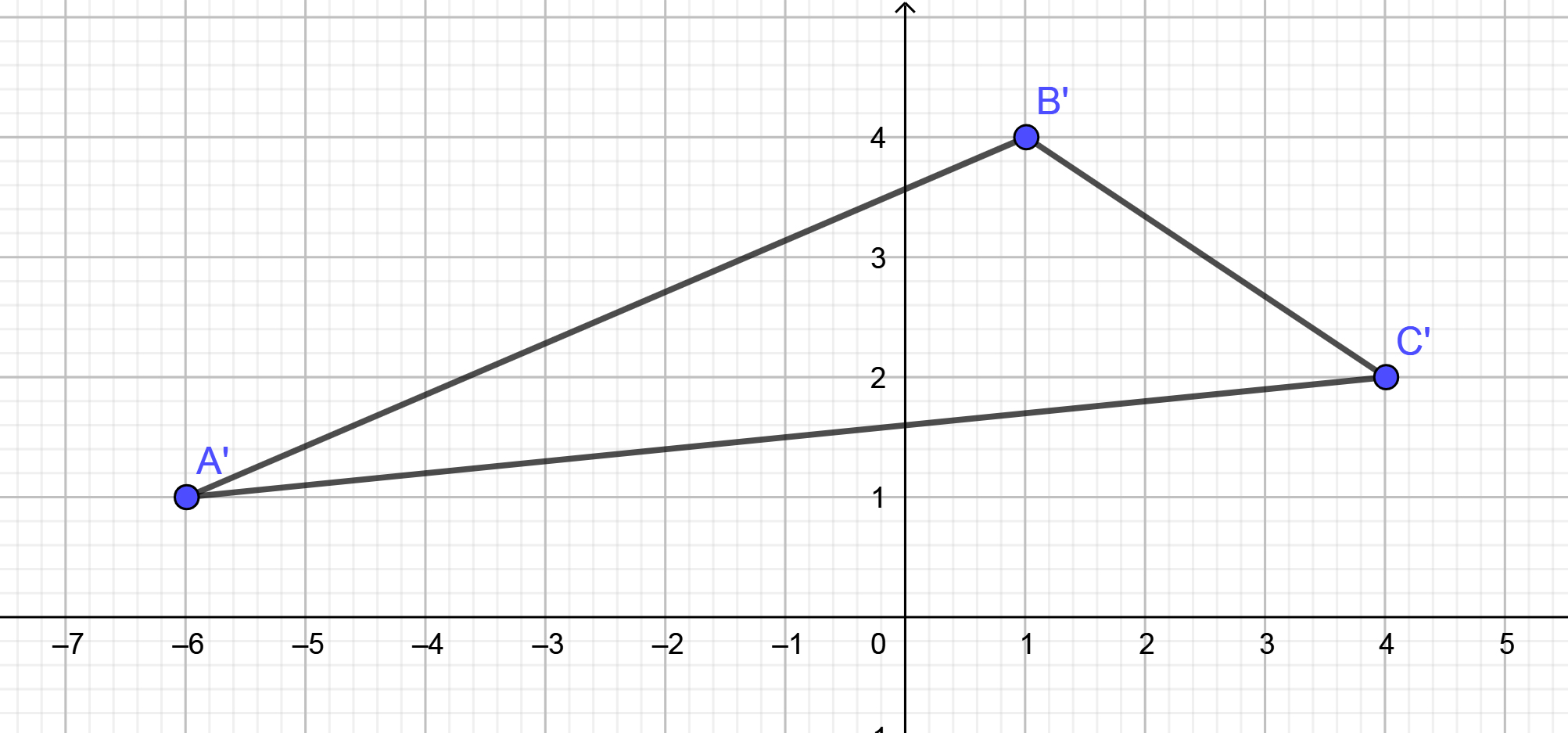
\( \mathrm{ A(-1,-6) \rightarrow A^\prime (-6,\ 1) } \) \( \mathrm{ B(-4,\ 1) \rightarrow B^\prime (1,\ 4) } \) \( \mathrm{ C(-2,\ 4) \rightarrow C^\prime (4,\ 2) } \) |
Create the graph. |
 |
Suppose an angle has a vertex of \(\left(-5,-10\right)\).
If this angle is rotated \(R_{-180^\circ}\) around the origin, name the coordinates of the image vertex.
In what quadrant is this ordered pair?
The image vertex is \(\left(5,10\right)\).
This ordered pair is in quadrant \(1\).
If you need help arriving at this answer, click the Solution button.
Apply the transformation \(R_{-180°}:\left(x,y\right)\rightarrow\)\(\left(-x,-y\right)\) to the vertex \(\left(-5,-10\right)\). |
\(\left(-5,-10\right)\rightarrow\left(5,10\right)\) |
Name the quadrant where \(\left(5,10\right)\) resides. |
Since both \(x\)- and \(y\)-coordinates of the vertex are positive, the image of the vertex is in quadrant \(1\). |
In the graph below, \(\overline{\text{AB}}\) is the preimage and \(\overline{\text{A}^\prime \text{B}^\prime}\) is the image.
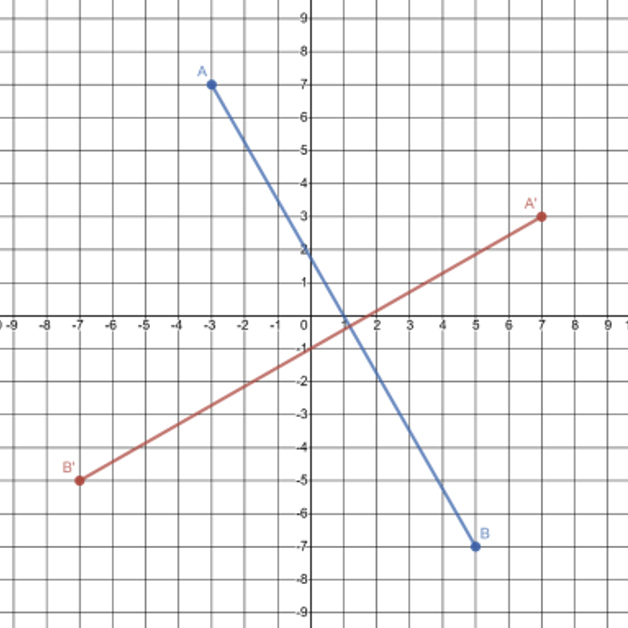
If the center of rotation is the origin, name the degree of clockwise rotation.
The degree of rotation is \(R_{-90^\circ}\).
If you need help arriving at this answer, click the Solution button.
Name the endpoints of the preimage. |
\(\text{A}\left(-3,7\right)\) \(\text{B}\left(5,-7\right)\) |
Name the endpoints of the image. |
\(\text{A}^\prime\left(7,3\right)\) \(\text{B}^\prime\left(-7,-5\right)\) |
Compare. |
\(\text{A}\left(-3,7\right)\rightarrow \text{A}^\prime\left(7,3\right)\) \(\text{B}\left(5,-7\right)\rightarrow \text{B}^\prime\left(-7,-5\right)\) Each pair of end points satisfies \(\left(x,y\right)\rightarrow\left(y,-x\right)\). In the clockwise direction, this means that the line segment was rotated \(90^\circ\). |
