So far, you have learned about rotating objects counterclockwise in the coordinate plane. Now it is time to learn how to rotate objects in the clockwise direction. Remember that counterclockwise movement is positive, and clockwise movement is negative.
In the video below, an instructor will demonstrate how to rotate objects when given a negative measure of rotation. As you watch the video, pay close attention to the process of performing a negative rotation in the coordinate plane.
You may want to use the study guide to follow along. If so, click below to download the study guide.
You've seen how to do positive rotations, that is rotations in the counterclockwise direction, but we also need to know how to do rotations in the negative, or clockwise, direction. Before we get to that, let's review the rules about rotations in the positive, counterclockwise direction. A rotation of 90 degrees follows the rule x, y maps to negative y, x. A rotation of 180 degrees follows the rule x, y maps to negative x, negative y. A rotation of 270 degrees follows the rule x, y maps to y, negative x. And a rotation of 360 degrees, which is a complete rotation, follows the rule x, y maps to x, y, because you've just returned the object to its original location. All these rules apply when we're rotating an object counterclockwise about the origin.
Now what about rotating objects in the negative direction, clockwise? The rules there are: a rotation of negative 90 degrees follows the rule x, y maps to y, negative x. A rotation of negative 180 degrees follows the rule x, y maps to negative x, negative y. A rotation of negative 270 degrees follows the rule x, y maps to negative y, x. And a rotation of negative 360 degrees, which is a complete clockwise rotation, follows the rule x, y maps to x, y. All these rules apply when we are rotating an object clockwise about the origin.
Well, this is a lot of rules to remember. Fortunately, there is less to remember that there might seem. Notice that the rule for a rotation of positive 90 degrees is the exact same as the rule for a rotation of negative 270 degrees. Similarly, a rotation of positive 180 degrees is the same as a rotation of negative 180 degrees, a rotation of positive 270 degrees is the same as a rotation of negative 90 degrees, and a rotation of positive 360 degrees is the same as negative 360 degrees.
Why is this? Well, if we look at a coordinate plane, we can see that rotating a given point 90 degrees in the counterclockwise direction produces the same result as rotating it 270 degrees in the clockwise direction. This is also the case for positive and negative 180, and positive 270 and negative 90. And just as a full counterclockwise rotation around the origin returns back to the original location, so too does a full clockwise rotation.
With these rules in mind, let's head over to the whiteboard to look at a few examples.
This first question reads, "Perform a rotation of our of R of negative 90 degrees on angle A. Use the origin as the center of rotation." Well this rotation, a rotation of negative 90 degrees, follows the rule, the point x, y maps to the point y, negative x. So let's write down the coordinates for each of these three points in our preimage. Point A has coordinates of 4, negative 5. Point B in our preimage has coordinates of 8, negative 6. And point C in our preimage has coordinates of 9, negative 1. Now we're going to use this rule to help us determine the coordinates of the points in our image, starting with point A prime. So the x-coordinate in our image is going to be the same as the y-coordinate from our preimage, which is negative 5, and then the second coordinate, the y-coordinate, will be the opposite of the x-coordinate from the preimage, so our x-coordinate was 4, so in our image, our y-coordinate is going to be negative 4. What about point B prime? Again, our first coordinate is going to be the y-coordinate, so negative 6, and our y-coordinate is going to be the opposite of the x-coordinate, so negative 8. And then point C prime, we're going to use the same rule, so our x-coordinate is going to be negative 1, and our y- coordinate is going to be the opposite of the original x-coordinate, so negative 9. Now that we have the three points in our image defined, we can plot them and draw this angle. So point A prime is at negative
5, negative 4, so that's right here. Point B prime is at negative 6, negative 8, so that is right there. And C prime is at negative 1 negative 9. So that's right there. And just as in our preimage, A prime is going to be the vertex, so our angle is going to look something like that. Alright, let's look at another one.
This one reads, "Rotate triangle JKL negative 180 degrees around the origin." Well the rule for a rotation of negative 180 degrees is that point x, y maps to point negative x, negative y. So let's determine the coordinates for each of the three points in our preimage, starting with point J, which has coordinates of negative 4, 1. Point K has coordinates of negative 3, 3. And point L has coordinates of negative 1, 1. Now we're going to use this rule to determine the points on our image. So point J prime is going to have coordinates of the opposite of the x-coordinate is going to be 4, and the opposite of 1 is negative 1, so 4, negative 1. What about K prime? We're going to just change the signs of each of these coordinates, so negative 3 becomes 3, and 3 becomes negative 3. And then L prime, negative 1 becomes 1 and 1 becomes negative 1. So those are the coordinates of the points that define the triangle that makes up our image. So let's plot these, starting with J prime, which is at point 4, negative 1, right there. Write J prime. K prime is at 3, negative 3, which is right here. We'll draw K prime. And then L prime is at 1, negative 1, so right here. That's L prime. And we connect those three points like this, and that is this triangle rotated negative 180 degrees, so 180 degrees in the clockwise direction, about the origin. Alright, let's look at one more example.
This one reads, "Perform a rotation of R of negative 270 degrees on line segment OP. Use the origin as the center of rotation." So when the origin is our center of rotation then a rotation of negative 270 degrees uses the rule x, y maps to point negative y, x. So let's determine the coordinates of the two points that define this segment, first with point O. Point O has coordinates of negative 3, negative 7, and point P has coordinates of 5, 8. So now let's determine the coordinates of the points O prime and P prime. Applying this rule, our first coordinate is going to be the opposite of the y-coordinate of the preimage, so that's negative 7 becomes 7. And then our second coordinate is going to be the x- coordinate from the preimage, and that is negative 3. For point P prime, we're going to do the same process, so our first coordinate, our x-coordinate, is going to be the opposite of the y-coordinate of the preimage. the y-coordinate of our preimage is 8, so that's going to be negative 8. And then the y- coordinate is going to be the x-coordinate from our preimage, which is 5. So now let's plot these two points. We'll start with point O prime at 7, negative 3. So that's 7, and then negative 3 right there. That's O prime. And then point P prime is at negative 8, 5. So negative 8, and then up 5, right there. So then we connect those two points with a line, and that is this line rotated 270 degrees, so that's 270 degrees clockwise like that, the negative direction.
Question
This graph shows the preimage of \(\triangle\text{JKL}\).
Preimage |
|---|
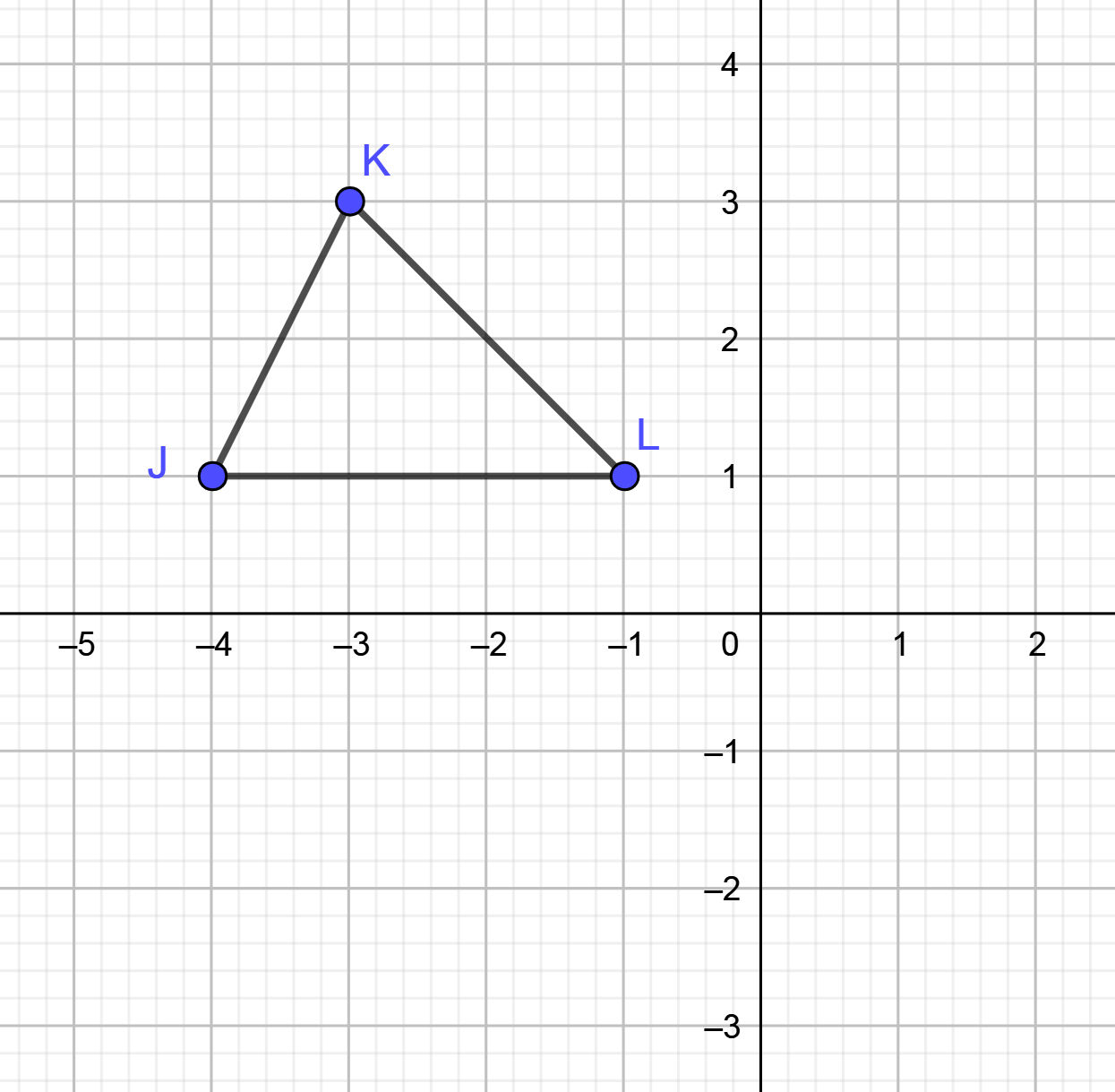 |
The graph on the left shows the image of \(\triangle\text{JKL}\) after a \(-180^\circ\) rotation around the origin. The graph on the right shows the image of \(\triangle\text{JKL}\) after a \(+180^\circ\) rotation around the origin.
\(-180^\circ\) Rotation |
\(+180^\circ\) Rotation |
|---|---|
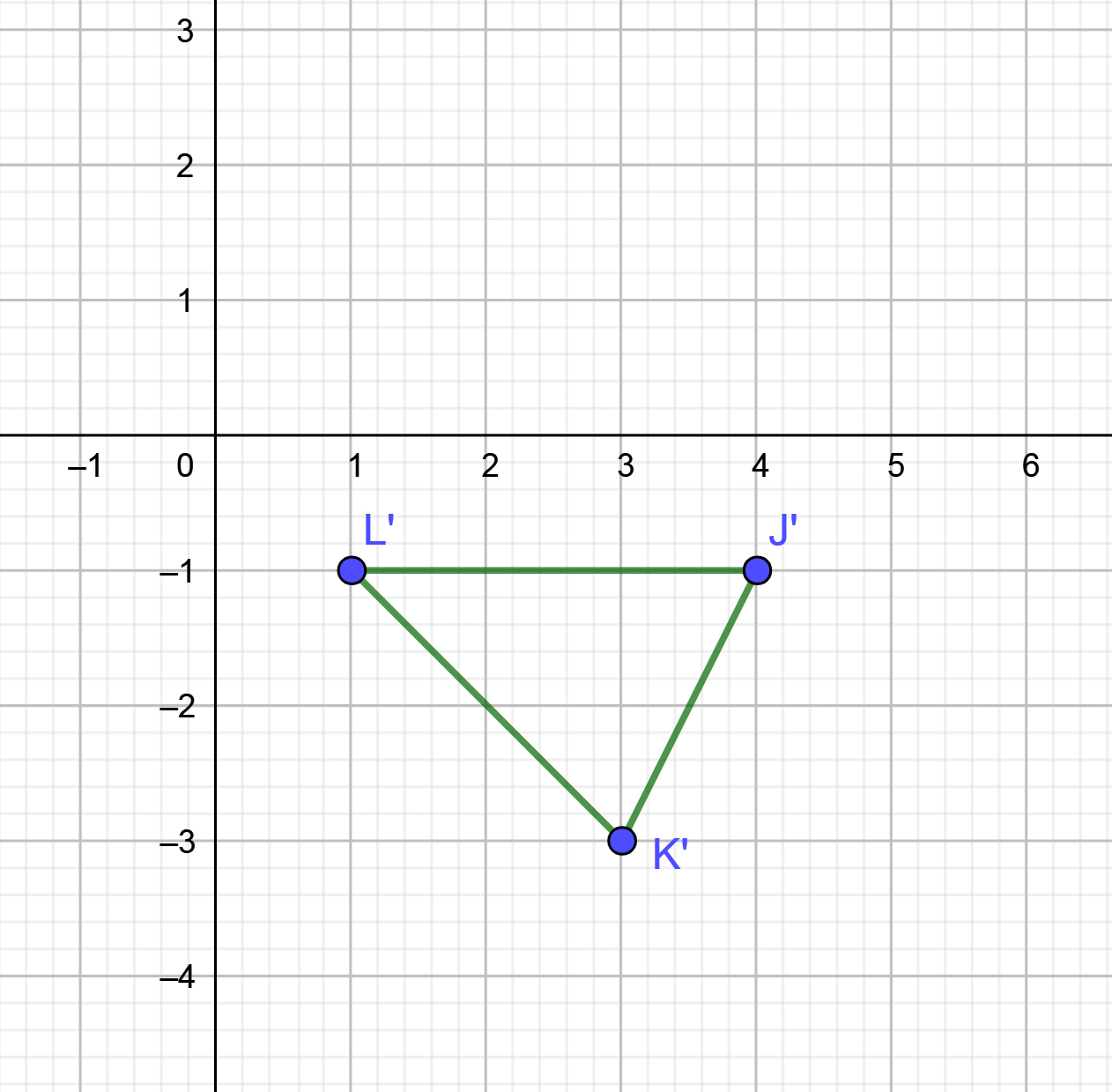 |
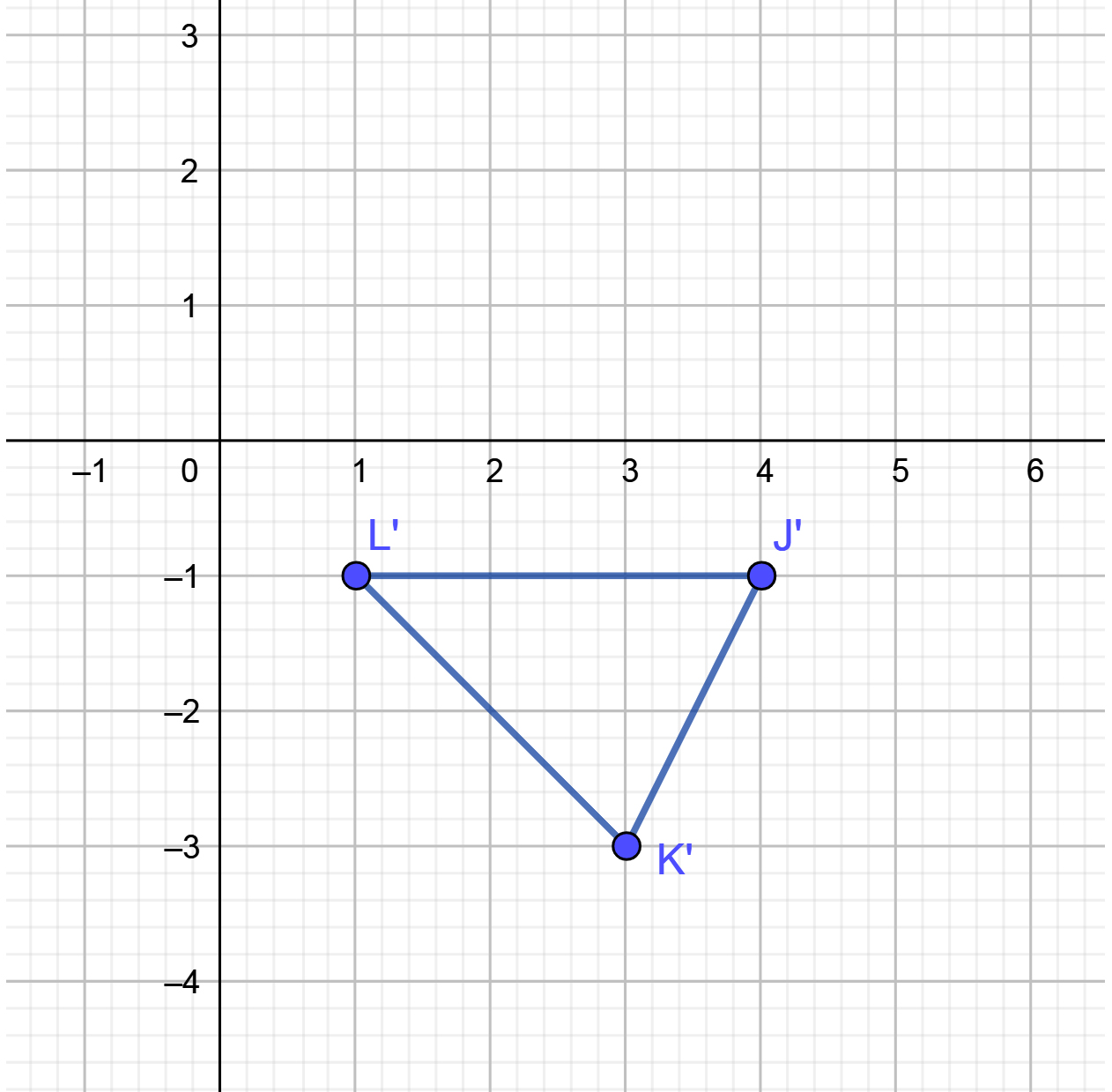 |
What do you notice about the two images of \(\triangle\text{JKL}\)? Be specific.
Rotating an object either \(-180^\circ\) or \(180^\circ\) results in the same image on the coordinate plane. A rotation of \(-180^\circ\) is the same as a rotation of \(+180^\circ;R_{-180^\circ}=R_{180^\circ}\).
