In this lesson, you have learned the notation and vocabulary you need to discuss the rotation of objects in the coordinate plane. You have also learned how to perform both counterclockwise and clockwise rotations in the coordinate plane. How these rotations transform ordered pairs that lie along objects is shown in the table below.
|
Counterclockwise Rotation (positive) |
Clockwise Rotation (negative) |
|---|---|
|
\(R_{90°}:\left(x,y\right)\rightarrow\left(-y,x\right)\) \(R_{180°}:\left(x,y\right)\rightarrow\left(-x,-y\right)\) \(R_{270°}:\left(x,y\right)\rightarrow\left(y,-x\right)\) \(R_{360°}:\left(x,y\right)\rightarrow\left(x,y\right)\) |
\(R_{-90°}:\left(x,y\right)\rightarrow\left(y,-x\right)\) \(R_{-180°}:\left(x,y\right)\rightarrow\left(-x,-y\right)\) \(R_{-270°}:\left(x,y\right)\rightarrow\left(-y,x\right)\) \(R_{-360°}:\left(x,y\right)\rightarrow\left(x,y\right)\) |
When you spin an object around a center of rotation in the coordinate plane, its preimage and image are congruent. Congruent objects have the same size and shape. You can show that two objects in the coordinate plane are a preimage and a rotated image. When this is true, then the two objects are congruent; and you can use rotations to map one object to the other. For example:
Use rotations to show that \(\triangle\text{ABC}\) and \(\triangle\text{A}^\prime\text{B}^\prime\text{C}^\prime\) are congruent. Assume the center of rotation is the origin.
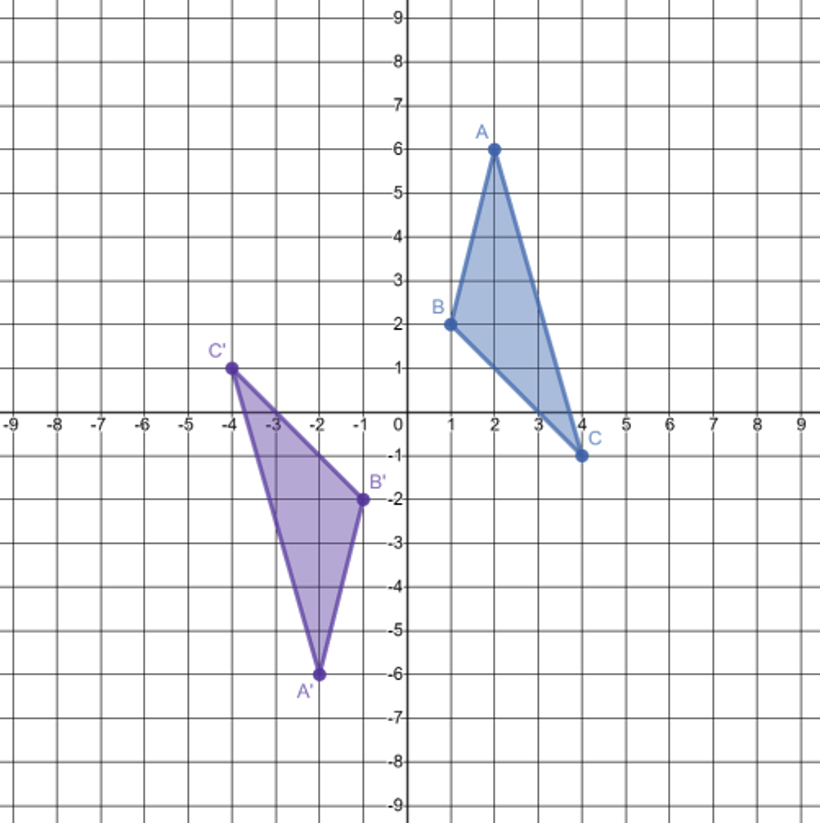
Two triangles drawn on a coordinate plane. The blue triangle has coordinates A(2, 3), B(1, 2), and C(4, negative 1). The purple triangle has coordinates A′(negative 2, negative 6), B′(negative 1, negative 2), C′(negative 4, 1).
|
Name the coordinates of the vertices of triangle ABC |
\(\text{A}\left(2,6\right)\) \(\text{B}\left(1,2\right)\) \(\text{C}\left(4,-1\right)\) |
|
Name the coordinates of the vertices of triangle \(\text{A}^\prime B^\prime C^\prime\). |
\(\text{A}^\prime\left(-2,-6\right)\) \(\text{B}’\left(-1,-2\right)\) \(\text{C}^\prime\left(-4,1\right)\) |
Compare. |
Since you can use the rotation \(R_{-180^\circ}:\left(x,y\right)\rightarrow\left(-x,-y\right)\) to map \(\text{A}\rightarrow\text{A}^\prime,\text{B}\rightarrow \text{B}^\prime,\) and \(\text{C}\rightarrow\text{C}^\prime\), the two triangles are a preimage and an image, and so they are congruent. Note that you can also use a rotation of positive \(180^\circ\)and the result is the same. |
Now it’s your turn! Use your knowledge of rotations to complete the activity below. Look at each graph and determine if it shows a preimage and its rotated image. Assume that the center of rotation is the origin. Click the graph to check your answer.
