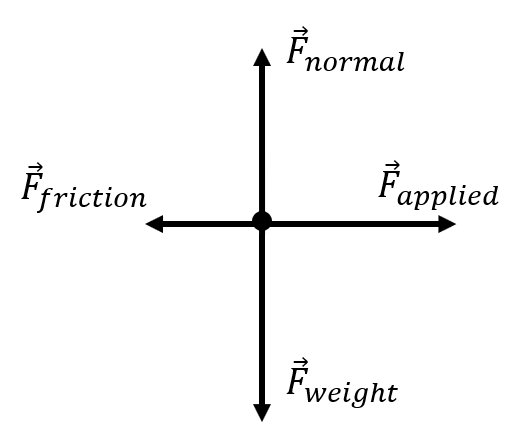
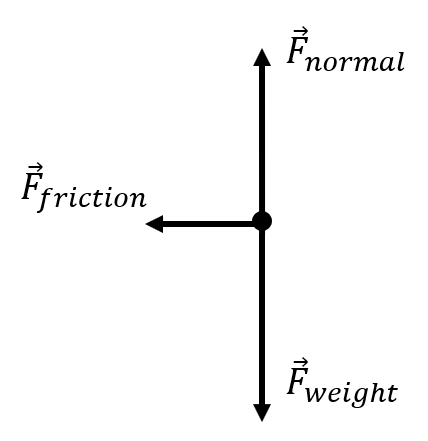
Solve these problems by first quantifying the forces, then finding the net force, then using Newton's Second Law, and finally any kinematics equations to find the missing values.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
| A block of wood whose mass is 5.00 kg rests on a horizontal floor. A horizontal force of 60.0 N is applied to the block. If the coefficient of kinetic friction is 0.520, what is the magnitude of the block's acceleration? |
|
\(\small\mathsf{ m = 5.00 kg }\) \(\small\mathsf{ \overrightarrow{F}_{applied} = 60 \text{ N} }\) \(\small\mathsf{ \mu_k = 0.520 }\) \(\small\mathsf{\overrightarrow{a} = ? }\) |
\(\small\mathsf{ \Sigma F = \overrightarrow{F}_{normal} + \overrightarrow{F}_{weight} = 0 }\) \(\small\mathsf{ F_{friction} = \mu F_{normal} }\) \(\small\mathsf{ \Sigma F = \overrightarrow{F}_{friction} + \overrightarrow{F}_{applied} = m \overrightarrow{a} }\) |
Find the normal force: \(\small\mathsf{ \overrightarrow{F}_{normal} = -(5.00 \text{ kg})(-9.81 \text{ m/s}^2) }\) \(\small\mathsf{ \overrightarrow{F}_{normal} = 49.05 \text{ N} }\) Find the force of friction: \(\small\mathsf{ F_{friction} = (0.520)(49.05 \text{ N}) }\) \(\small\mathsf{ F_{friction} = 25.506 \text{ N} }\) Find the acceleration: \(\small\mathsf{-25.506 \text{ N} + 60.0 \text{ N} = (5.00 \text{ kg}) \overrightarrow{a} }\) \(\small\mathsf{34.494 \text{ N} = (5.00 \text{ kg}) \overrightarrow{a} }\) \(\small\mathsf{\overrightarrow{a} = \frac{34.494 \text{ N}}{5.00 \text{ kg}} }\) \(\small\mathsf{\overrightarrow{a} = 6.90 \text{ N} }\) |
| A forklift pushes a 600.0 kg wooden pallet across the floor at a constant velocity of 0.540 m/s. The coefficient of kinetic friction is 0.280. After the forklift stops pushing the pallet, how long does it take the pallet to stop moving? |
|
\(\small\mathsf{ m = 600.0 kg }\) \(\small\mathsf{ \mu_k = 0.280 }\) \(\mathsf{ \overrightarrow{v}_i = 0.540 \text{ m/s} }\) \(\mathsf{ \overrightarrow{v}_f = 0 \text{ m/s} }\) \(\mathsf{ t = ? }\) |
\(\small\mathsf{ \Sigma F = \overrightarrow{F}_{normal} + \overrightarrow{F}_{weight} = 0 }\) \(\small\mathsf{ F_{friction} = \mu F_{normal} }\) \(\small\mathsf{ \overrightarrow{F_{net}} = m \overrightarrow{a} }\) \(\mathsf{\overrightarrow{a} = \frac{\overrightarrow{v}_f - \overrightarrow{v}_i}{t} }\) |
Find the normal force: \(\small\mathsf{ \overrightarrow{F}_{normal} = -(600.0 \text{ kg})(-9.81 \text{ m/s}^2) }\) \(\small\mathsf{ \overrightarrow{F}_{normal} = 5886 \text{ N} }\) Find the force of friction: \(\small\mathsf{ F_{friction} = (0.280)(5886 \text{ N}) }\) \(\small\mathsf{ F_{friction} = 1648.08 \text{ N} }\) The force of friction becomes the net force: \(\small\mathsf{ 1648.08 \text{ N} = (600.0 \text{ kg})\overrightarrow{a} }\) \(\small\mathsf{ \overrightarrow{a} = \frac{-1648.08 \text{ N}}{600.0 \text{ kg}} }\) \(\small\mathsf{ \overrightarrow{a} = -2.75 \text{ m/s}^2 }\) Use the acceleration in the kinematics equation to find time: \(\small\mathsf{-2.75 \text{ m/s}^2 = \frac{0 - 0.540 \text{ m/s}}{t} }\) \(\small\mathsf{ t = \frac{-0.540 \text{ m/s}}{-2.75 \text{ m/s}^2} }\) \(\small\mathsf{ t = 0.196 \text{ s} }\) |
| A 14 kg box slides to a stop in 3.0 seconds having travelled 6.0 meters. What is the coefficient of kinetic friction? [Hint: work through the steps backwards.] |
|
\(\small\mathsf{ m = 14 kg }\) \(\mathsf{ \overrightarrow{d} = 6.0 \text{ m} }\) \(\mathsf{ \overrightarrow{v}_f = 0 \text{ m/s} }\) \(\mathsf{ t = 6.0 \text{ s} }\) \(\small\mathsf{ \mu_k = ? }\) |
\(\small\mathsf{\overrightarrow{d} = \frac{1}{2}(v_i + v_f)t }\) \(\mathsf{\overrightarrow{a} = \frac{\overrightarrow{v}_f - \overrightarrow{v}_i}{t} }\) \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) \(\small\mathsf{ \Sigma F = \overrightarrow{F}_{normal} + \overrightarrow{F}_{weight} = 0 }\) \(\small\mathsf{ \mu = \frac{F_{friction}}{F_{normal}} }\) |
Find the initial velocity: \(\small\mathsf{6.0 \text{ m} = \frac{1}{2}(v_i + 0)(3.0 \text{ s}) }\) \(\small\mathsf{12.0 \text{ m} = (v_i)(3.0 \text{ s}) }\) \(\small\mathsf{v_i = \frac{12.0 \text{ m}}{3.0 \text{ s}} }\) \(\small\mathsf{v_i = 4.0 \text{ m/s} }\) Find the acceleration: \(\small\mathsf{\overrightarrow{a} = \frac{0 - 4.0 \text{ m/s}}{3.0 \text{ s}} }\) \(\small\mathsf{\overrightarrow{a} = -1.33 \text{ m/s}^2 }\) Find the net force, which is equal to the force of friction: \(\small\mathsf{ \overrightarrow{F} = (14 \text{ kg})(-1.33 \text{ m/s}^2) }\) \(\small\mathsf{ \overrightarrow{F} = -18.67 \text{ N} }\) Find the normal force: \(\small\mathsf{ \overrightarrow{F}_{normal} = -(14 \text{ kg})(-9.81 \text{ m/s}^2) }\) \(\small\mathsf{ \overrightarrow{F}_{normal} = 137.34 \text{ N} }\) Find the coefficient of kinetic friction: \(\small\mathsf{ \mu = \frac{18.67 \text{ N}}{137.34 \text{ N}} }\) \(\small\mathsf{ \mu = 0.14 }\) |