You can use some basic steps for writing and solving equations to find the measures of angle pairs. They are shown below.
- Identify the type of angle pair. Remember that angles can be complementary, supplementary, linear, adjacent, or vertical.
- Identify the facts about the angle pair. Ask yourself, "How do these facts affect the angles shown?"
- Set up an equation to solve, making sure to use the correct facts about the specific angle pairs.
- Solve the equation for the unknown variable.
- Substitute the value of the unknown variable into the given equation to find the measure of the unknown angle.
Take Note
You will not always need to use Step 5.
Practice solving for angle values using the activity below. Read and answer the question on each tab. Then click the answer button to check your response.
If the \(\text{m} \angle \text{ABD = 56°}\), then solve for \( x \) and find \(\text{m} \angle \text{1}\).
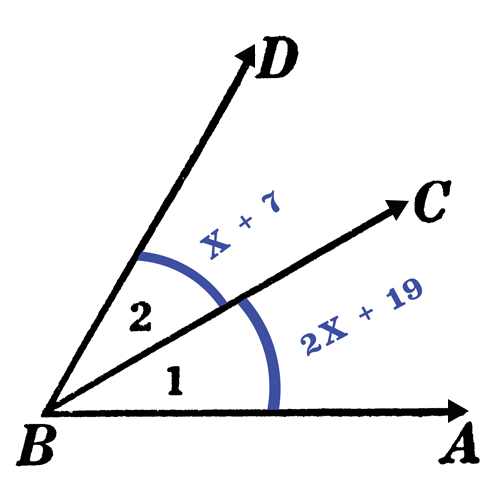
An angle consisting of two angles. The two angles share a vertex and a side and do not overlap each other. Angle 1 is labelled with the equation 2x+19 Angle 2 is labelled with the equation x+7.
\( x =\) 10
\(\text{m} \angle 1 = 39^{\circ}\)
If you need help arriving at this answer, click the solution button.
Step 1: Identify the type of angle pair. Angles can be complementary, supplementary, linear, adjacent, or vertical. |
These angles share a common vertex and a common side. They are adjacent angles. |
Step 2: Identify the facts about the angle pair. Ask yourself, "How do these facts affect the angles shown?" |
The sum of the measures of the two adjacent angles will be the measure of the larger angle. |
Step 3: Set up an equation to solve, making sure to use the correct facts about the specific angle pairs. |
Since the \(\text{m} \angle \text{ABD} = 56^{\circ} \), then \(\text{m} \angle 1 + \text{m}\angle 2 = 56^{\circ} \) \((x +7) + (2 x + 19) = 56\) |
Step 4: Solve the equation for the unknown variable. |
\((x + 7) + (2x + 19) = 56\) \(x + 7 + 2x + 19 = 56\) \(x + 2 + 7 + 19 = 56\) \(3x + 26 = 56\) \(3x = 30\) \(x = 10\) |
Step 5: Substitute the value of the unknown variable into the given equation to find the measure of the unknown angle. |
Substitute \(x\) into the expression for angle 1. \(\text{m} \angle 1 = \) \(2x + 19\) \(\text{m} \angle 1 = \) \(2(10) + 19\) \(\text{m} \angle 1 = \) \(20 + 19\) \(\text{m} \angle 1 = 39^{\circ}\) |
Find the measure of an unknown angle that is complementary to \(\text{m} \angle \text{XYZ}\), if the \(\text{m} \angle \text{XYZ = 72°}\)
The measure of the unknown angle is 18°
If you need help arriving at this answer, click the solution button.
Step 1: Identify the type of angle pair. Angles can be complementary, supplementary, linear, adjacent, or vertical. |
You are told the two angles are complementary angles. |
Step 2: Identify the facts about the angle pair. Ask yourself, "How do these facts affect the angles shown?" |
Complementary angles sum to 90°. |
Step 3: Set up an equation to solve, making sure to use the correct facts about the specific angle pairs. |
You can use any variable to represent the unknown angle measure. We'll use \(z\). \(z + 72 = 90\) |
Step 4: Solve the equation for the unknown variable. |
\(z + 72 = 90\) \(z = 18^{\circ}\) |
Find the value of \(y\), and then find the value of \(x\).
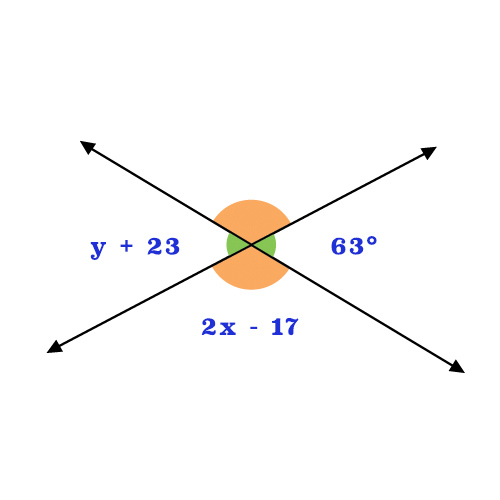
Two lines that intersect each other to form an X shape and four angles. The top angle is not labelled. The angle on the left is labelled with the equation y+23 The bottom angle is labelled with the equation 2x-17. The angle on the right is labelled 63 degrees.
\(y = 40\)
\(x = 67\)
If you need help arriving at this answer, click the solution button.
Step 1: Identify the type of angle pair. |
In the illustration, intersecting lines form two nonadjacent angles. These are vertical angles. Notice that \(y + 23\) is directly opposite the \(63^{\circ}\)angle. Also notice that \(2x − 17\) and the \(63^{\circ}\) angle share a common vertex and a common side. These are a linear pair. |
First, find the value of \(y\).
Step 2: Identify the facts about the angle pair. |
\(y + 23\) and the \(63^{\circ}\)angle are vertical angles. Vertical angles are congruent, which means that they measure the same number of degrees. |
Step 3: Set up an equation to solve. |
\(y + 23 = 63\) |
Step 4: Solve the equation for the unknown variable. |
\(y + 23 = 63\) \(y = 40\) |
Now, find the value of \(x\).
Step 2: Identify the facts about the angle pair. |
\(2x − 17\) and the \(63^{\circ}\) angle are a linear pair. Linear pairs are supplementary, which means their measures sum to 180°. |
Step 3: Set up an equation to solve. |
\(2x − 17 + 63 = 180\) |
Step 4: Solve the equation for the unknown variable. |
\(2x − 17 + 63 = 180\) \(2x + 46 = 180\) \(2x = 134\) \(x = 67\) |
Find the \(\text{m} \angle \text{KMH}\)
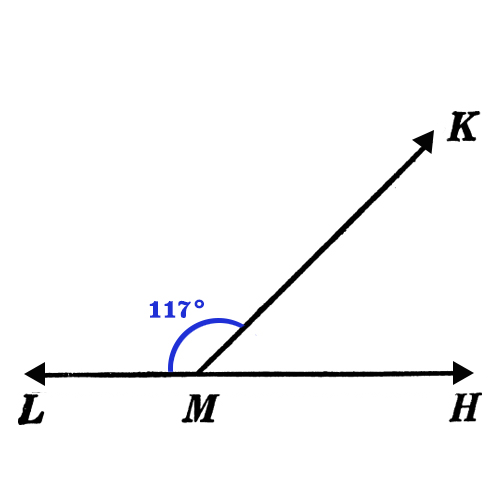
A 180 degree angle consisting of angle KML and angle KMH. angle KML is labelled 117 degrees.
\(\text{m} \angle \text{KMH} = 63^{\circ}\)
If you need help arriving at this answer, click the solution button.
Step 1: Identify the type of angle pair. |
Angle LMH is a straight angle, so \(\angle \text{KML}\) and \(\angle \text{KMH}\) must be supplementary. |
Step 2: Identify the facts about the angle pair. |
Supplementary angles sum to \(180^{\circ}\). |
Step 3: Set up an equation to solve. |
\(\text{117}^{\circ} + \text{m}\angle \text{KMH} = 180^{\circ}\) |
Step 4: Solve the equation for the unknown variable. |
\(117^{\circ} + \text{m}\angle \text{KMH} = 180^{\circ}\) \(\text{m}\angle \text{KMH} = 63^{\circ}\) |
