You have practiced categorizing single angles based on their degree measure. The main types of angles include acute, right, obtuse, and straight.
But more commonly angles appear in pairs. In geometry, angle pairs can have special relationships based on their measures and their orientation. There are four main types of angle pairs. Click each tab to learn about each one.
If you join a sports team with other players who are very skilled, but have very different strengths from your own, then you're probably headed for a winning season! Your different strengths compensate for any weaknesses on the team, and complement each other well.
Angles, too, can complement each other.
Complementary angles are two angles whose measurements that sum to exactly 90°.
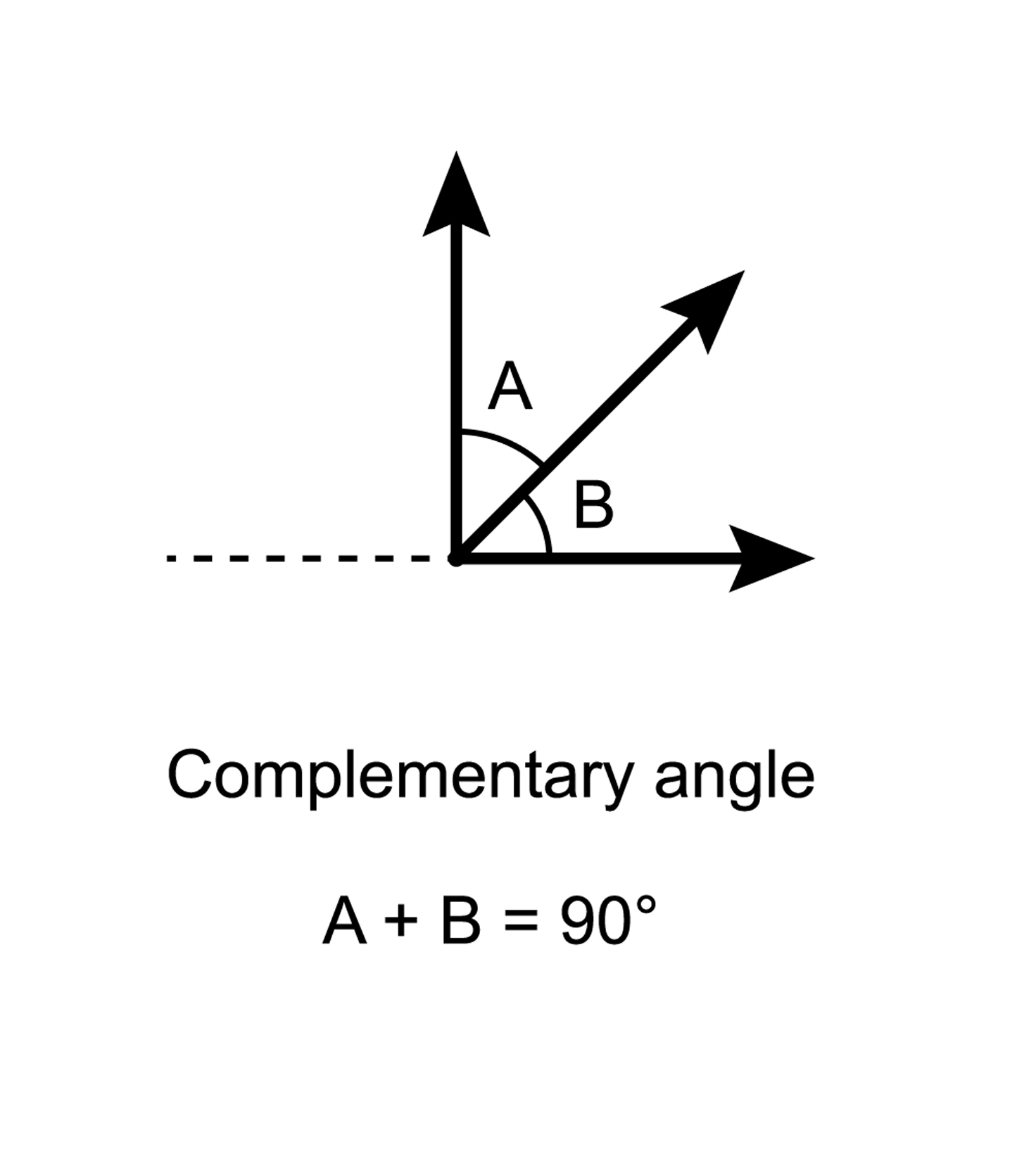
A 90 degree angle consisting of two angles labelled A and B. The equation A+B = 90 degrees appears at the bottom of the image.
Keep in Mind
Complementary angles do not have to be congruent. Complementary angles also do not have to be touching or be side by side.
Use what you have just learned about complementary angles to respond to the questions in the table. When you think you know the angle measurement, click the question to check.
| Question | Answer | Calculation |
|---|---|---|
60º |
90º – 30º = 60º |
|
35º |
90º – 55º = 35º |
Have you ever taken vitamins? Vitamins contain nutrients in them that can be added to the nutrients that we get from food. Thus, we can say that vitamins supplement our daily intake of nutrients.

Angles, too, can supplement each other.
Supplementary angles are two angle measurements that sum to exactly 180°. When the two angles that sum to 180° share a common vertex and a common side, then they are also considered to be linear pairs.
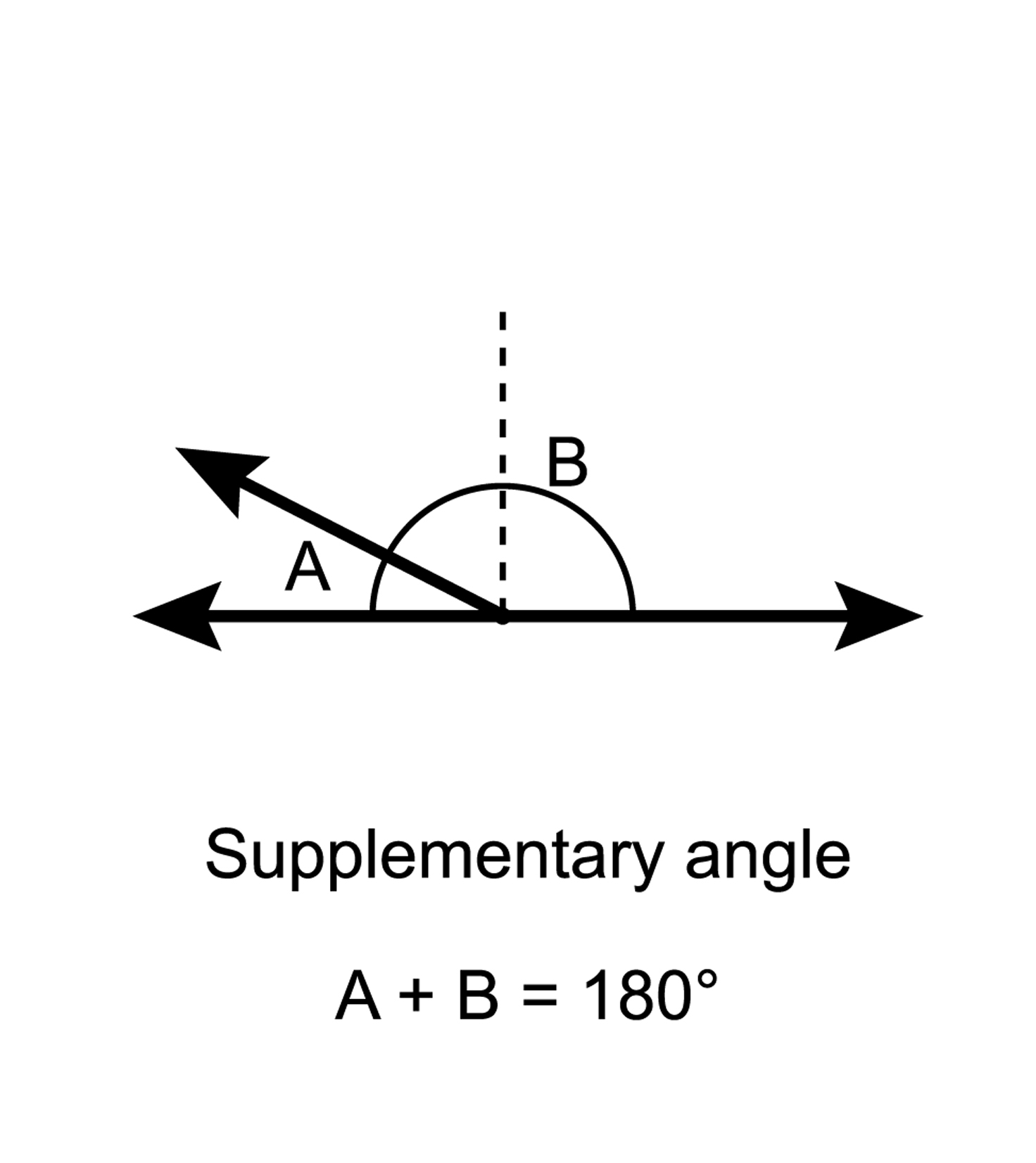
A 180 degree angle consisting of two angles labelled A and B. The equation A+B = 180 degree appears at the bottom of the image.
Keep in Mind
Two angles that are supplementary do not have to be the same size or touching. However, they must be touching, or share a common side and vertex, to be considered a linear pair.
Use what you have just learned about supplementary angles to respond to the questions in the table. When you think you know the angle measurement, click the question to check.
| Question | Answer | Calculation |
|---|---|---|
110º |
180º – 70º = 110º |
|
5º |
180º – 175º = 5º |
Have you ever gone to the movie theatre with a group of friends? Did you and your friends sit separately, or did you sit beside each other like the friends in this photo? These friends are occupying adjacent seats in a movie theatre. The word "adjacent" means "next to" or "neighboring".

Angles, too, can be adjacent.
Adjacent angles share a common vertex and a common side. These angles do not overlap each other. If angles are a linear pair, then they are also adjacent angles.
Angles that are not adjacent are called nonadjacent angles. The terms adjacent and nonadjacent describe how close angles are to each other. Think about the seats in a movie theater. If someone occupies the seat right next to yours, then you are seats are adjacent. Nonadjacent angles have their own "seats" which are apart from each other.
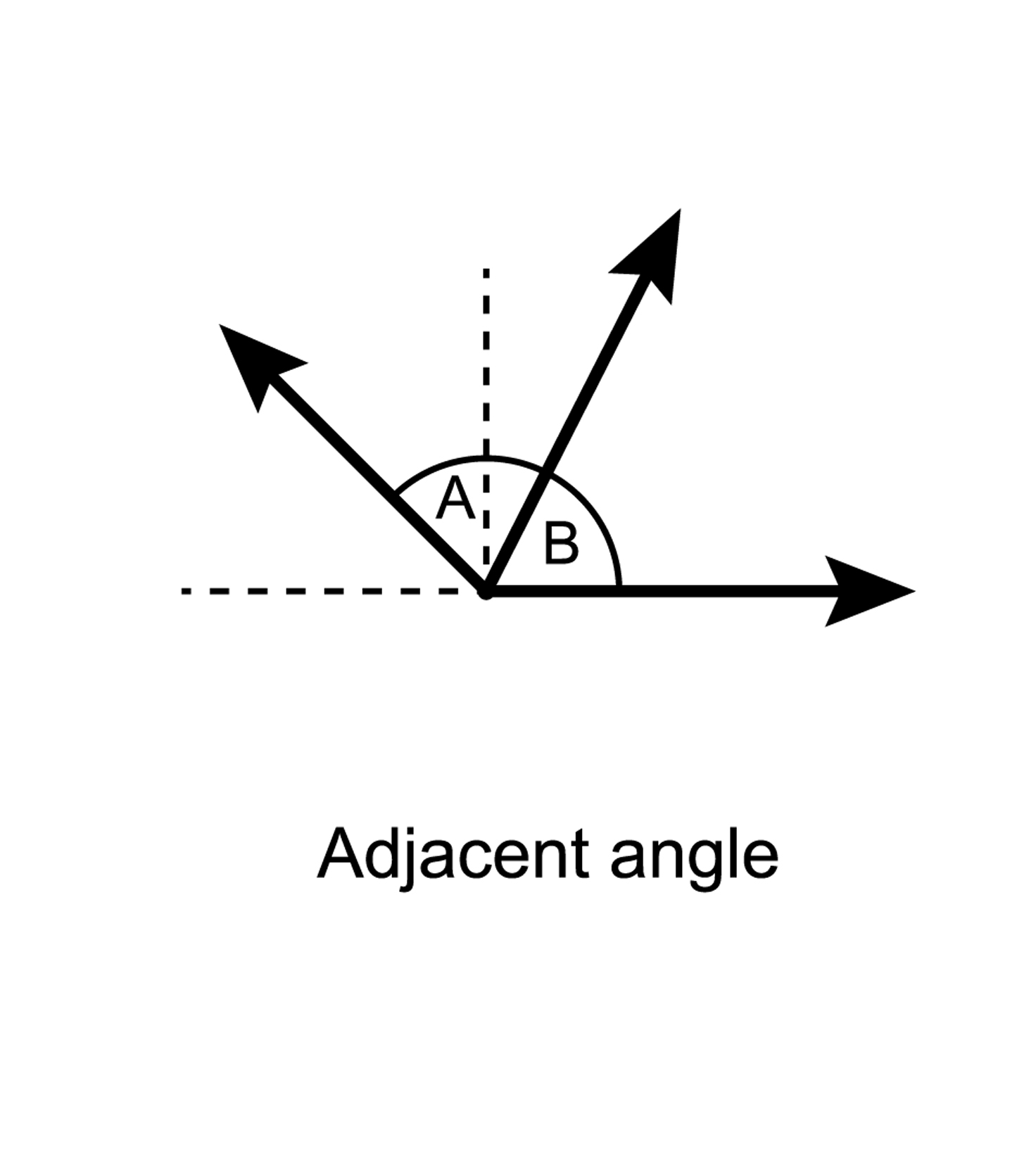
An angle consisting of two angles labelled A and B. The two angles share a vertex and a side and do not overlap each other.
Keep in Mind
Unlike complementary or supplementary angles, the measure of adjacent angles do not sum to a certain degree. However, when two angles are adjacent and they sum to 90°, then they are complementary angles. If two angles are adjacent and sum to 180°, then they are supplementary angles.
Angles that do not share a common side are called nonadjacent angles. When intersecting lines form two nonadjacent angles, then those angles are called vertical angles.
In this image, \(\angle \text{A}\) and \(\angle \text{B}\) are one pair of vertical angles.
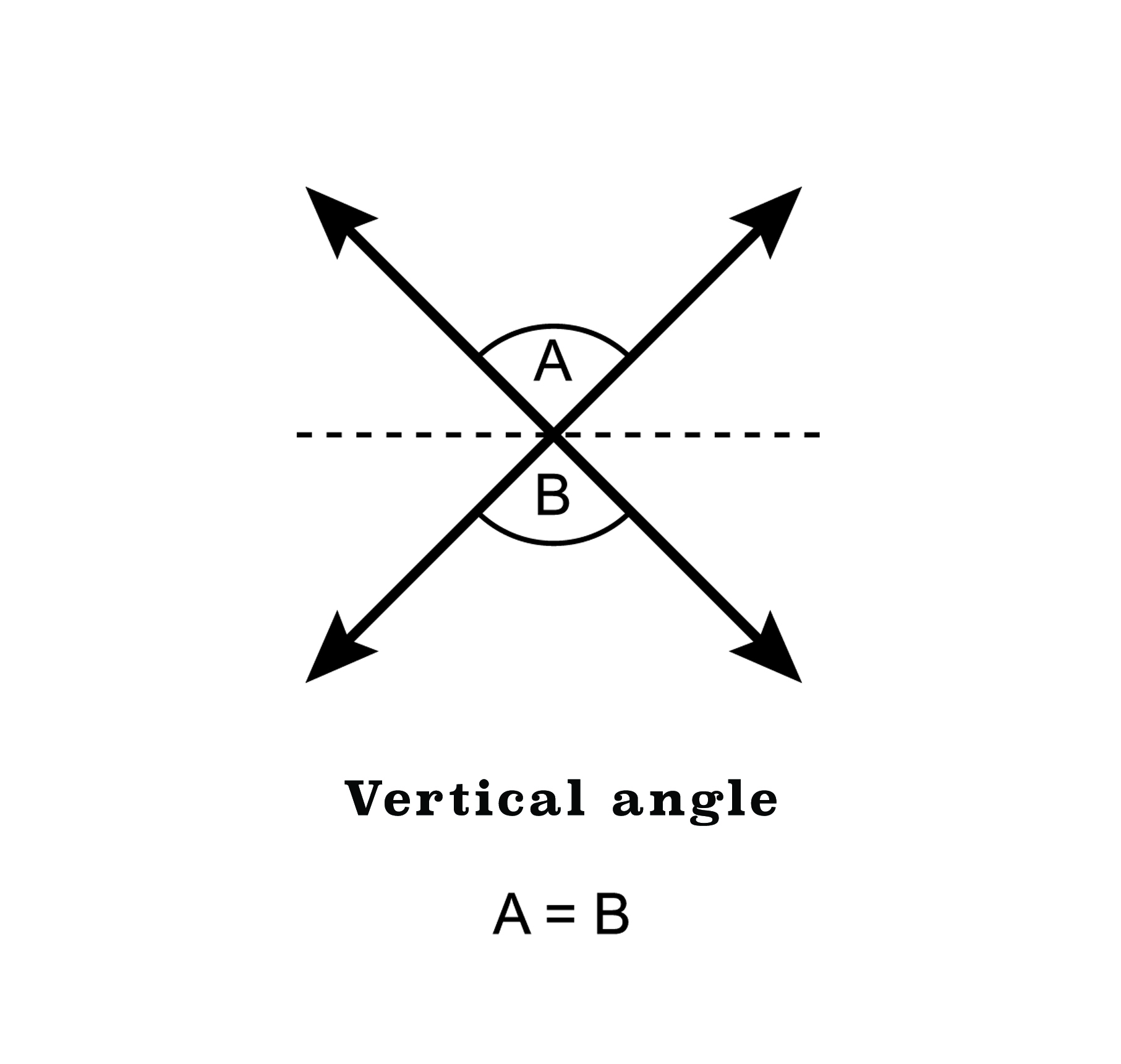
Two lines that intersect each other to form an X shape and four angles. The top angle is labelled A and the bottom angle is labelled B. The other two angles are not labelled. The equation A=B appears at the bottom of the image.
Keep in Mind
Vertical angles are always congruent. Their angle measures are identical.
Test your knowledge of the relationships that exist among pairs of angles by completing the activity below. Match each image on the left with its best classification on the right.
