
You can use the graph of a line to create a related table of values. This table shows you some of the ordered pairs that lie along the line in the coordinate plane. A table of values is often more helpful for writing the related linear equation than the graph.
Remember that a linear equation is an equation with an independent and a dependent variable. You learned about two different forms linear equations can take: \( y = kx \) and \( y = x + b \). Review these forms by reading the information in the rows below.
Some linear equations have the form \( y = kx \).
In this form, \( y \) represents the dependent variable, and \( x \) is the independent variable.
The value of \( x \) is multiplied by \( k \).
The variable \( k \) can be any number other than 0.
The equations \( y = 10x, \) \( y = - 8x \), and \( y = \frac{1}{2}x \) are all examples of equations in this form.
The graph of \( y = 10x \) is shown.
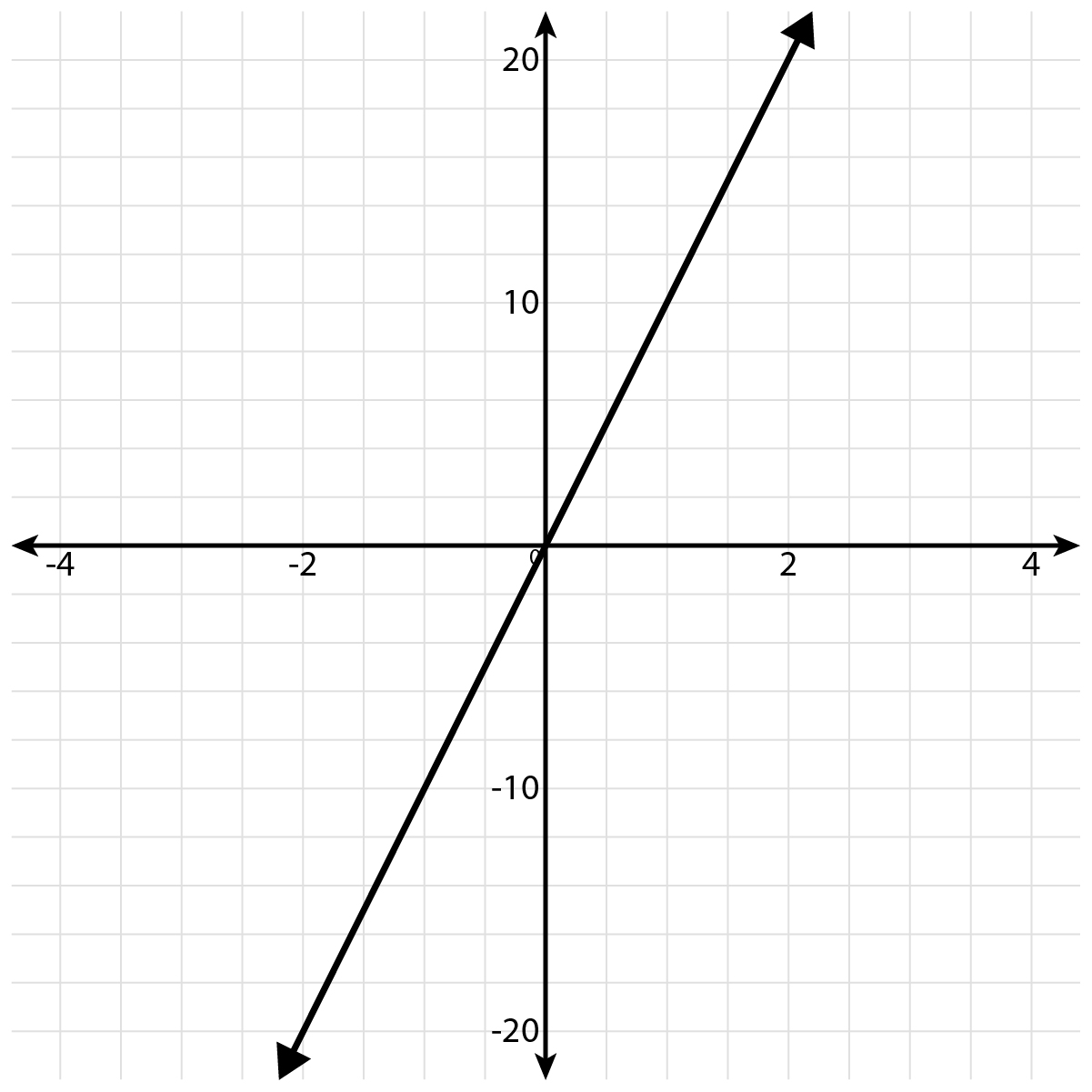
A graph of the equation y = 10x on a coordinate plane that goes through the ordered pairs (−1, −10), (0, 0), and (1, 10).
This line passes through the origin.
Linear equations of the form \( y = kx \) always pass through or touch the ordered pair \( (0,\ 0) \).
The table of values for a graph of an equation in this form is a ratio table.
Linear equations can also look like \( y = x + b \).
In this form, \( y \) represents the dependent variable, and \( x \) is the independent variable.
Notice that the value of \( x \) is multiplied by 1. You add the value of \( b \) to \( x \).
The equations \( y = x + 10, \) \( y = x - 8 \), and \( y = x + \frac{1}{2} \) are all examples of equations in this form.
The graph of \( y = x + 10 \) is shown.

A graph of the equation y = x + 10 on a coordinate plane that goes through the ordered pairs (−2, 8), (0, 10), and (2, 12).
This line crosses over the \( y \)-axis at an ordered pair that is not the origin.
The table of values for a graph of an equation in this form is NOT a ratio table.
It is important to understand the different forms of a linear equation, how to work with each, and what the graph of each kind of equation looks like. You can practice these skills with the activity below. Click the equation or statement that does not belong in each set.
Which does not belong?
1. Which is NOT a form of a linear equation?
\( y = x^{2} + b \)
\( \displaystyle y = x + b \)
\( \displaystyle y = kx \)
Linear equations can have the form \( y = kx \) or \( y = x + b \).
Linear equations can have the form \( y = kx \) or \( y = x + b \).
Linear equations can have the form \( y = kx \) or \( y = x + b \).
2. Which equation is NOT in \( y = kx \) form?
\( \displaystyle y = - 7x \)
\( y = x - 8 \)
\( \displaystyle y = \frac{1}{4}x \)
The equations \( y = 10x, \) \( y = - 8x \), and \( y = \frac{1}{2}x \) are all examples of equations in this form.
The equations \( y = 10x, \) \( y = - 8x \), and \( y = \frac{1}{2}x \) are all examples of equations in this form.
The equations \( y = 10x, \) \( y = - 8x \), and \( y = \frac{1}{2}x \) are all examples of equations in this form.
3. Which equation is NOT in \( y = x + b \) form?
\( \displaystyle y = x + \frac{3}{5} \)
\( \displaystyle y = x - 8 \)
\( \displaystyle y = \frac{1}{4}x \)
The equations \( y = x + 10, \) \( y = x - 8 \), and \( y = x + \frac{1}{2} \) are all examples of equations in this form.
The equations \( y = x + 10, \) \( y = x - 8 \), and \( y = x + \frac{1}{2} \) are all examples of equations in this form.
The equations \( y = x + 10, \) \( y = x - 8 \), and \( y = x + \frac{1}{2} \) are all examples of equations in this form.
4. Which statement about the graph of an equation in \( y = kx \) form is NOT true?
The equation graphs as a straight line.
The graph of the equation passes through the ordered pair \( (0,\ 0) \).
The graph of the equation is a circle.
When an equation is in \( y = kx \) form, the graph of the straight line touches or passes through the origin.
When an equation is in \( y = kx \) form, the graph of the straight line touches or passes through the origin.
When an equation is in \( y = kx \) form, the graph of the straight line touches or passes through the origin.
5. Which statement about the table of values for the graph of a line in \( y = x + b \) form is NOT true?
The table of values contains ordered pairs that lie along the line.
The table of values is a ratio table.
The table of values does not contain the ordered pair \( (0,\ 0) \).
The table of values for a graph of an equation in this form is NOT a ratio table.
The table of values for a graph of an equation in this form is NOT a ratio table.
The table of values for a graph of an equation in this form is NOT a ratio table.
You got # out of # correct. Click the Retry button for another attempt.
You got a perfect score. Great job!
