The steps to create a table of values from the graph of a line and then write the related linear equation are shown below.
- Create the table of values using the ordered pairs on the line.
- Use the graph and table of values to help you decide which kind of linear equation to use.
- Use the table of values to find the pattern in the ordered pairs.
- Write the linear equation.
- Check your work.
Practice these skills with the activity below. Respond to the question on each tab. When you are ready, you can click the Answer button to check your work. Remember that you can refer to the examples on the previous page if you need help.
Use the graph shown to create a table of values. Then use the table of values to write the related linear equation.
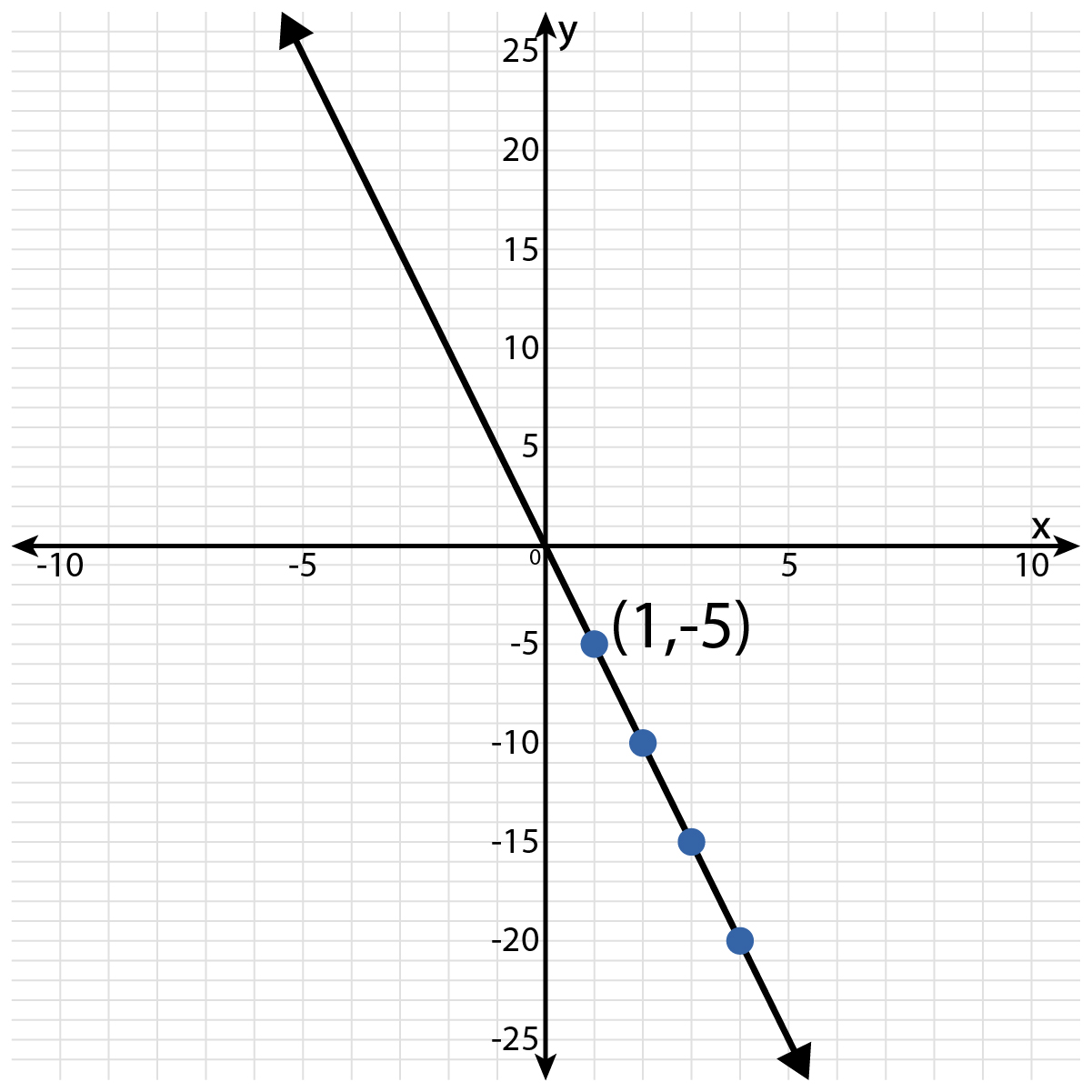
A linear graph decreases from left to right through the point (1, −5).
The horizontal axis is scaled by ones, and the vertical axis is scaled by fives.
A table of values is shown. The linear equation is \( y = - 5x \).
| \( \displaystyle x \) | \( \displaystyle y \) |
|---|---|
\( \displaystyle 1 \) |
\( \displaystyle - 5 \) |
\( \displaystyle 2 \) |
\( \displaystyle - 10 \) |
\( \displaystyle 3 \) |
\( \displaystyle - 15 \) |
\( \displaystyle 4 \) |
\( \displaystyle - 20 \) |
If you need help arriving at this answer, click the Solution button below.
Step 1: Create the table of values using the ordered pairs on the line. |
The axes are labeled as \( x \) and \( y \). There is one labeled ordered pair: \( (1, - 5) \). Read the coordinates of the points that are marked with a dot using the axes. Create the table of values.
The \( x \) represents the independent variable. The \( y \) represents the dependent variable. |
|||||||||||||||
Step 2: Use the graph and table of values to help you decide which kind of linear equation to use. |
The graph shows a straight line that passes through the origin. The equation will have the form \( y = kx \). |
|||||||||||||||
Step 3: Use the table of values to find the pattern in the ordered pairs. |
The ordered pairs listed on the graph and in the table are \( (1, - 5) \), \( (2, - 10) \), \( (3, - 15) \), and \( (4, - 20) \). Is there a number you can multiply each \( x \)-value by to arrive at the \( y \)-value?
In each case, you can multiply the \( x \)-value by \( - 5 \) to arrive at the \( y \)-value. The value of \( k \) is \( - 5 \). |
|||||||||||||||
Step 4: Write the equation. |
Use the form of the equation you identified in Step 2 and the pattern from Step 3. \( \displaystyle y = - 5x \) |
|||||||||||||||
Step 5: Check your work. |
Use substitution to check your work. When \( x = 1 \): \( \displaystyle y = - 5\left( 1 \right) \) \( y = - 5 \) When \( x = 2 \): \( \displaystyle y = - 5\left( 2 \right) \) \( y = - 10 \) You can check the remaining \( x \)-values to see that multiplying each of them by \( - 5 \) leads you to the needed \( y \)-value. The equation is correct. |
Use this graph to create a table of values. Then use the table of values to write the related linear equation.
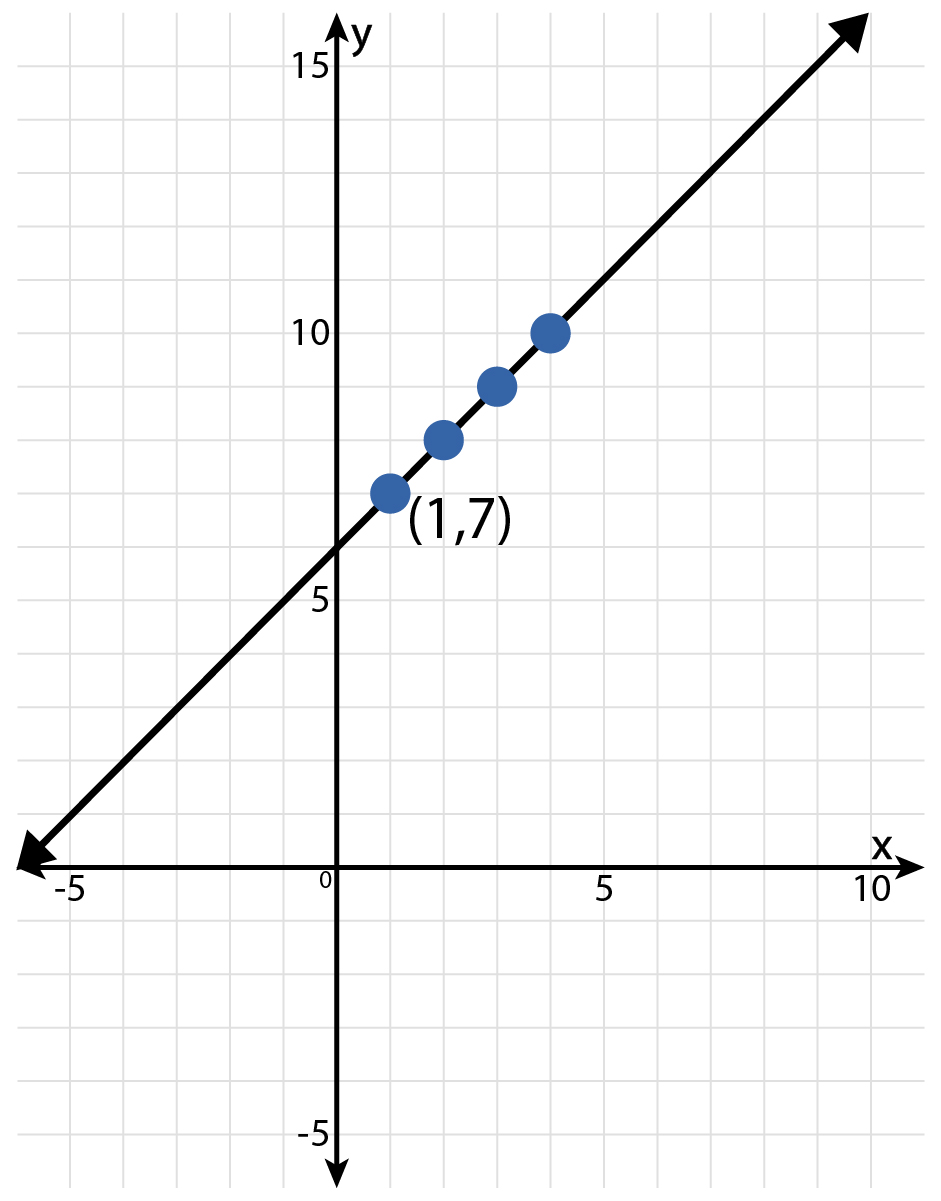
A linear graph increases from left to right through the point (1, 7).
A table of values is shown. The linear equation is \( y = x + 6 \).
| \( \displaystyle x \) | \( \displaystyle y \) |
|---|---|
\( \displaystyle 1 \) |
\( \displaystyle 7 \) |
\( \displaystyle 2 \) |
\( \displaystyle 8 \) |
\( \displaystyle 3 \) |
\( \displaystyle 9 \) |
\( \displaystyle 4 \) |
\( \displaystyle 10 \) |
If you need help arriving at this answer, click the Solution button below.
Step 1: Create the table of values using the ordered pairs on the line. |
The axes are labeled as \( x \) and \( y \). There is one labeled ordered pair: \( (1,\ 7) \). Read the coordinates of the points that are marked with a dot using the axes. Create the table of values.
The \( x \) represents the independent variable. The \( y \) represents the dependent variable. |
|||||||||||||||
Step 2: Use the graph and table of values to help you decide which kind of linear equation to use. |
The graph shows a straight line that does NOT pass through the origin. The equation will have the form \( y = x + b \). |
|||||||||||||||
Step 3: Use the table of values to find the pattern in the ordered pairs. |
The ordered pairs listed on the graph and in the table are \( (1,\ 7) \), \( (2,8) \), \( (3,9) \), and \( (4,10) \). Is there a number you can add to each \( x \)-value to arrive at the \( y \)-value?
In each case, you can add \( 6 \) to the \( x \)-value to arrive at the \( y \)-value. The value of \( b \) is \( 6 \). |
|||||||||||||||
Step 4: Write the equation. |
Use the form of the equation you identified in Step 2 and the pattern from Step 3. \( \displaystyle y = x + 6 \) |
|||||||||||||||
Step 5: Check your work. |
Use substitution to check your work. When \( x = 1 \): \( \displaystyle y = \left( 1 \right) + 6 \) \( y = 7 \) When \( x = 2 \): \( \displaystyle y = \left( 2 \right) + 6 \) \( y = 8 \) You can check the remaining \( x \)-values to see that adding 6 to each of them leads you to the needed \( y \)-value. The equation is correct. |
Mr. Alden is taking attendance prior to leaving on the field trip. Once everyone is on the buses, he notices there are 4 more students than they originally planned for. The graph reflects this information.
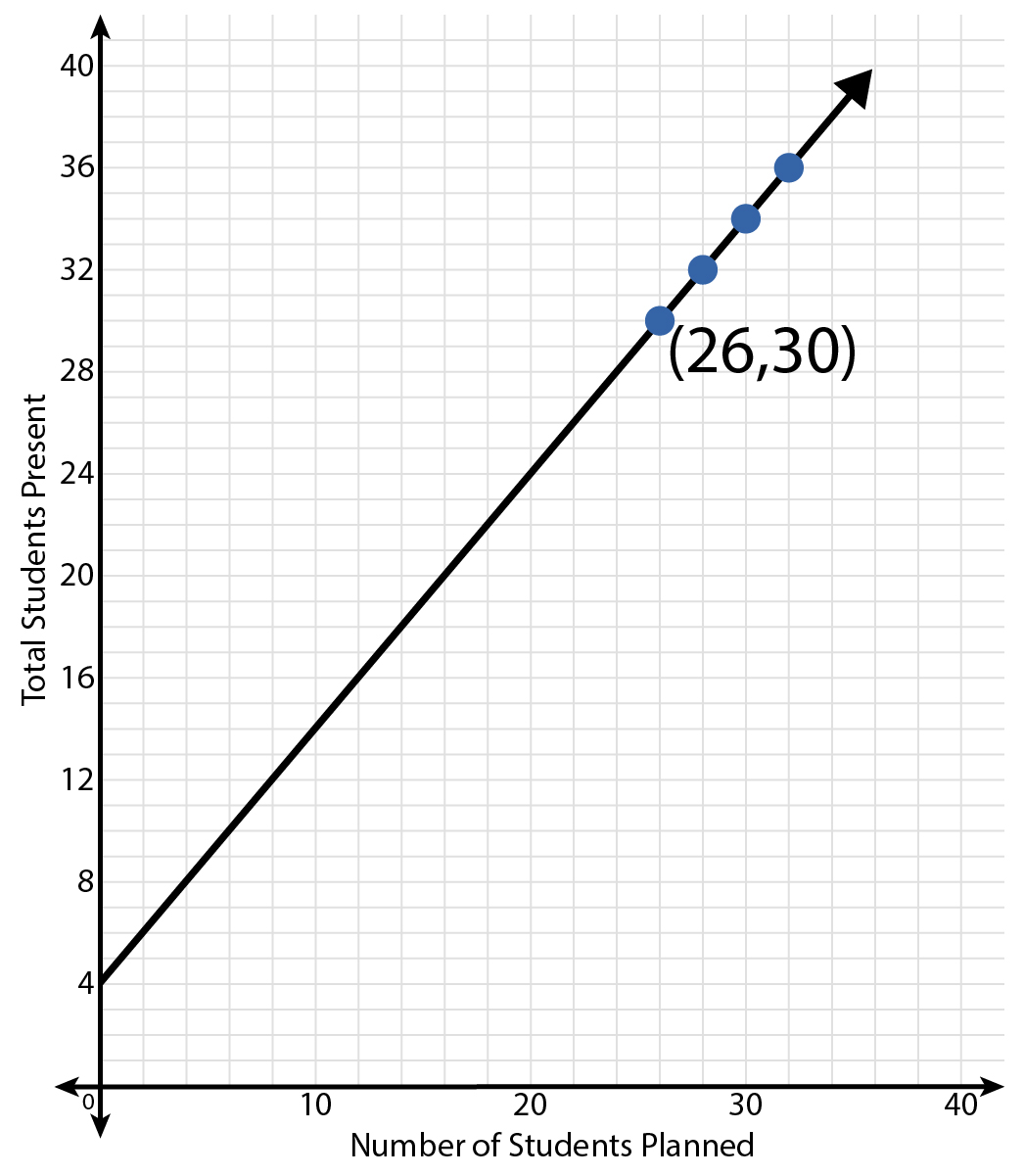
A coordinate plane with the following attributes:
- The x-axis is labeled Number of Students Planned.
- The y-axis is labeled Total Students Present.
- A line extends from (4, 0) through the ordered pair (26, 30).
Use the graph to create a table of values. Then use the table of values to write the related linear equation.
A table of values is shown. The linear equation is \( y = x + 4 \).
| Number of Students Planned, \( x \) | Total Students Present, \( y \) |
|---|---|
\( \displaystyle 26 \) |
\( \displaystyle 30 \) |
\( \displaystyle 28 \) |
\( \displaystyle 32 \) |
\( \displaystyle 30 \) |
\( \displaystyle 34 \) |
\( \displaystyle 32 \) |
\( \displaystyle 36 \) |
If you need help arriving at this answer, click the Solution button below.
Step 1: Create the table of values using the ordered pairs on the line. |
The axes are labeled as "Number of Students Planned" and "Total Students Present." There is one labeled ordered pair: \( (26,\ 30) \). Read the coordinates of the points that are marked with a dot using the axes. Create the table of values.
The \( x \) represents the independent variable. The \( y \) represents the dependent variable. |
|||||||||||||||
Step 2: Use the graph and table of values to help you decide which kind of linear equation to use. |
The graph shows a straight line that does NOT touch the origin. The equation will have the form \( y = x + b \). |
|||||||||||||||
Step 3: Use the table of values to find the pattern in the ordered pairs. |
The ordered pairs listed on the graph and in the table are \( (26,\ 30) \), \( (28,\ 32) \), \( (30,\ 34) \), and \( (32,\ 36) \). Is there a number you can add to each \( x \)-value to arrive at the \( y \)-value?
In each case, you can add \( 4 \) to the \( x \)-value to arrive at the \( y \)-value. The value of \( b \) is \( 4 \). |
|||||||||||||||
Step 4: Write the equation. |
Use the form of the equation you identified in Step 2 and the pattern from Step 3. \( \displaystyle y = x + 4 \) |
|||||||||||||||
Step 5: Check your work. |
Use substitution to check your work. When \( x = 26 \): \( \displaystyle y = \left( 26 \right) + 4 \) \( y = 30 \) When \( x = 28 \): \( \displaystyle y = \left( 28 \right) + 4 \) \( y = 32 \) You can check the remaining \( x \)-values to see that adding 4 to each of them leads you to the needed \( y \)-value. The equation is correct. |
Use this graph to create a table of values. Then use the table of values to write the related linear equation.
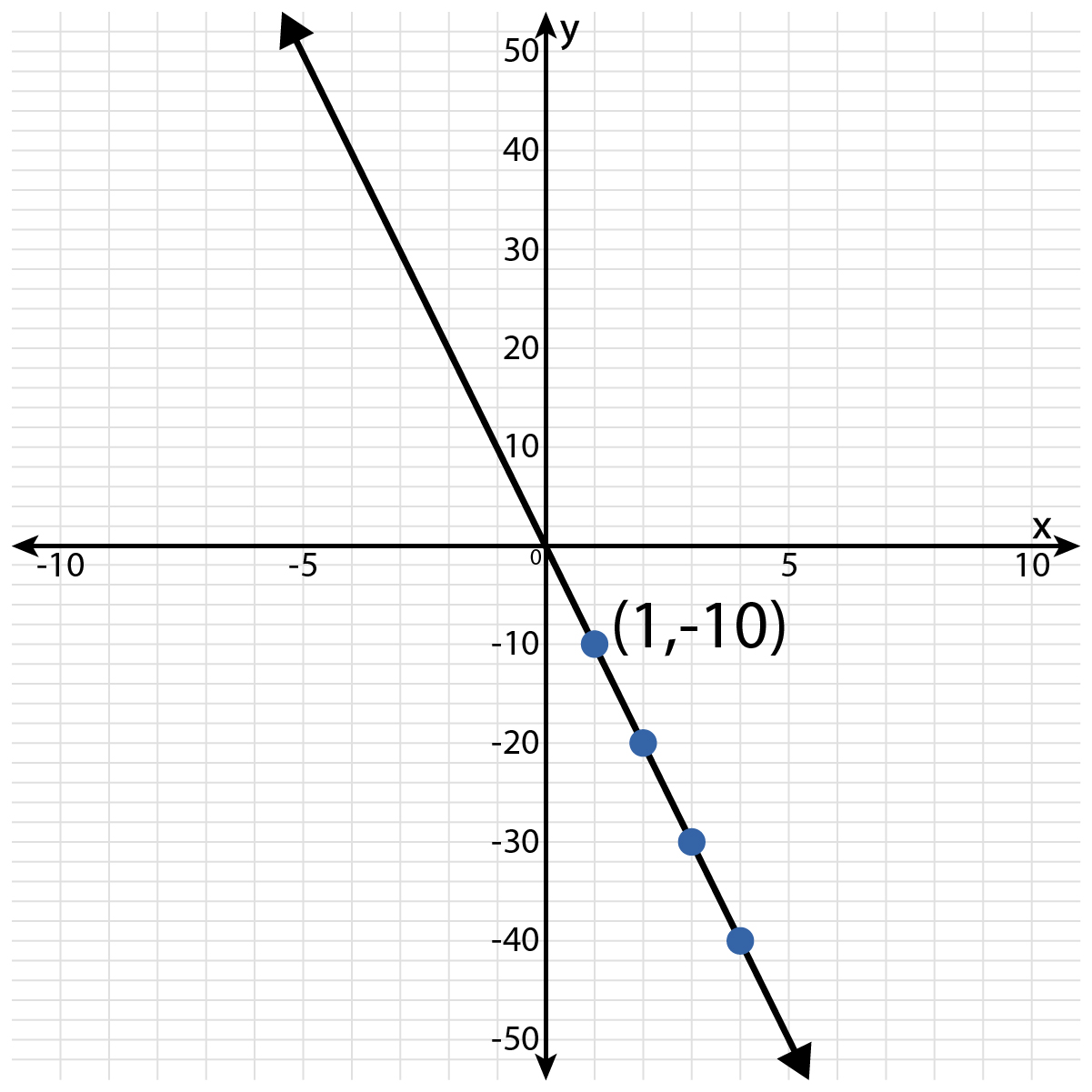
A linear graph decreases from left to right through the ordered pair (1, −10).
A table of values is shown. The linear equation is \( y = - 10x \).
| \( \displaystyle x \) | \( \displaystyle y \) |
|---|---|
\( \displaystyle 1 \) |
\( \displaystyle - 10 \) |
\( \displaystyle 2 \) |
\( \displaystyle - 20 \) |
\( \displaystyle 3 \) |
\( \displaystyle - 30 \) |
\( \displaystyle 4 \) |
\( \displaystyle - 40 \) |
If you need help arriving at this answer, click the Solution button below.
Step 1: Create the table of values using the ordered pairs on the line. |
The axes are labeled as \( x \) and \( y \). There is one labeled ordered pair: \( (1, - 10) \). Read the coordinates of the points that are marked with a dot using the axes. Create the table of values.
The \( x \) represents the independent variable. The \( y \) represents the dependent variable. |
|||||||||||||||
Step 2: Use the graph and table of values to help you decide which kind of linear equation to use. |
The graph shows a straight line that passes through the origin. The equation will have the form \( y = kx \). |
|||||||||||||||
Step 3: Use the table of values to find the pattern in the ordered pairs. |
The ordered pairs listed on the graph and in the table are \( (1, - 10) \), \( (2, - 20) \), \( (3, - 30) \), and \( (4, - 40) \). Is there a number you can multiply each \( x \)-value by to arrive at the \( y \)-value?
In each case, you can multiply the \( x \)-value by \( - 10 \) to arrive at the \( y \)-value. The value of \( k \) is \( - 10 \). |
|||||||||||||||
Step 4: Write the equation. |
Use the form of the equation you identified in Step 2 and the pattern from Step 3. \( \displaystyle y = - 10x \) |
|||||||||||||||
Step 5: Check your work. |
Use substitution to check your work. When \( x = 1 \): \( \displaystyle y = - 10(1) \) \( y = - 10 \) When \( x = 2 \): \( \displaystyle y = - 10\left( 2 \right) \) \( y = - 20 \) You can check the remaining \( x \)-values to see that multiplying each of them by \( - 10 \) leads you to the needed \( y \)-value. The equation is correct. |
Rita reads a magazine while on the way to the museum of natural history. Each issue of this favorite magazine has 8 pages of ads. The remaining pages contain the magazine content.
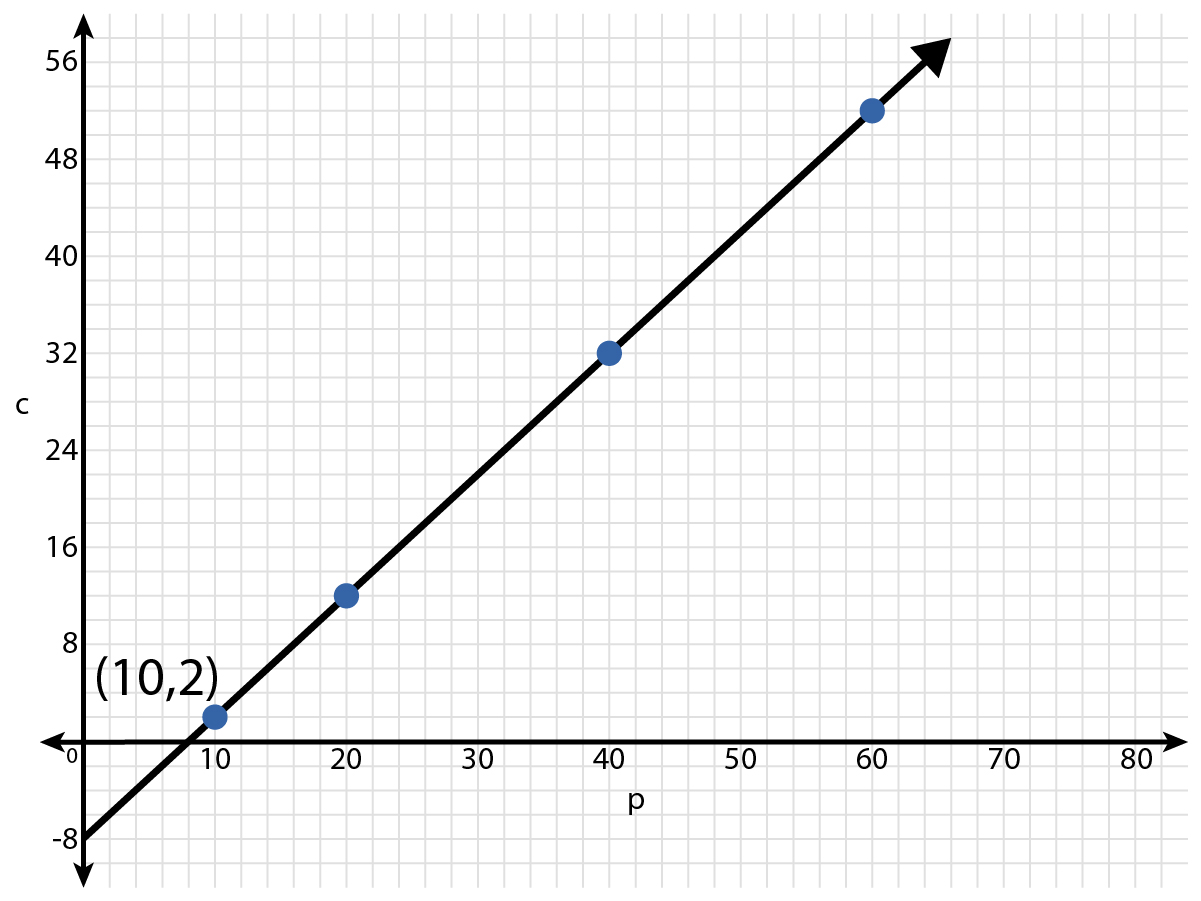
A linear graph increases from left to right through the ordered pair (10, 2).
Use the graph shown to create a table of values. Then use the table of values to write the related linear equation.
Pay close attention to how the axes are labeled. The variable \( p \) represents the total number of pages in a magazine, and \( c \) represents the number of content pages.
A table of values is shown. The linear equation is \( c = p + ( - 8) \).
| \( \displaystyle p \) | \( \displaystyle c \) |
|---|---|
\( \displaystyle 10 \) |
\( \displaystyle 2 \) |
\( \displaystyle 20 \) |
\( \displaystyle 12 \) |
\( \displaystyle 40 \) |
\( \displaystyle 32 \) |
\( \displaystyle 60 \) |
\( \displaystyle 52 \) |
If you need help arriving at this answer, click the Solution button below.
Step 1: Create the table of values using the ordered pairs on the line. |
The axes are labeled as \( c \) and \( p \). There is one labeled ordered pair: \( (10,\ 2) \). Read the coordinates of the points that are marked with a dot using the axes. Create the table of values.
The \( p \) represents the independent variable. The \( c \) represents the dependent variable. |
|||||||||||||||
Step 2: Use the graph and table of values to help you decide which kind of linear equation to use. |
The graph shows a straight line that does NOT touch or pass through the origin. The equation will have the form \( y = x + b \). |
|||||||||||||||
Step 3: Use the table of values to find the pattern in the ordered pairs. |
The ordered pairs listed on the graph and in the table are \( (10,\ 2) \), \( (20,\ 12) \), \( (40,\ 32) \), and \( (60,\ 52) \). Is there a number you can add to each \( p \)-value to arrive at the \( c \)-value?
In each case, you can add \( - 8 \) to the \( p \)-value to arrive at the \( c \)-value. The value of \( b \) is \( - 8 \). |
|||||||||||||||
Step 4: Write the equation. |
Use the form of the equation you identified in Step 2 and the pattern from Step 3. \( \displaystyle c = p + ( - 8) \) |
|||||||||||||||
Step 5: Check your work. |
Use substitution to check your work. When \( p = 10 \): \( \displaystyle c = (10) + ( - 8) \) \( c = 2 \) When \( p = 20 \): \( \displaystyle c = (20) + ( - 8) \) \( c = 12 \) You can check the remaining \( p \)-values to see that adding \( - 8 \) to each of them leads you to the needed \( c \)-value. The equation is correct. |
