The steps to solve one-step equations are shown below.
- Identify the inverse of the operation that is with the variable.
- Set up the inverse operation on both sides of the equation.
- Simplify both sides of the equation.
- Check the solution using substitution.
- Plot the solution on a number line if requested.
Solving equations is a skill that takes a lot of practice to master. As you have seen, equations can contain integers and rational numbers, as well as any of the operations addition, subtraction, multiplication, or division. As you read through the questions in the tabs below, make sure you carefully examine the equation before you start solving. And always check your work using substitution! When you are ready to check your response, you can click the Answer button.
If you need graph paper, click below to download printable graph paper in Word or PDF format.
Willem is at the grocery store with his dad. They plan to make some apple pies for a family gathering. They need 15 apples in all. Willem's dad bought 8 apples.
The equation \( a + 8 = 15 \) models this scenario, where \( a \) represents the number of apples they already had at home.

Solve the equation \( a + 8 = 15 \) for \( a \).
\( a = 7 \) apples
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( a + 8 = 15 \) has addition on the same side of the equal sign as the variable. The inverse is subtraction. |
Step 2: Set up the inverse operation on both sides of the equation. |
Subtract 8 from both sides of the equation. \( \displaystyle a + 8 = 15 \) \( \displaystyle a + 8\bbox[yellow]{- 8} = 15\bbox[yellow]{- 8} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. \( \displaystyle a + 8\bbox[yellow]{- 8} = 15\bbox[yellow]{- 8} \) \( \displaystyle a + 0 = 15\bbox[yellow]{- 8} \) \( \displaystyle a = 15\bbox[yellow]{- 8} \) Simplify the right-hand side of the equation. \( \displaystyle a = 15\bbox[yellow]{- 8} \) \( a = 7 \) apples |
Step 4: Check the solution using substitution. |
Substitute \( a = 7 \) into the original equation. Then simplify. \( \displaystyle \left( 7 \right) + 8 = 15 \) \( 15 = 15 \) |
Step 5: Plot the solution on a number line if requested. |
This step was not requested. You can skip it for this problem. |
Solve the equation \( 3 = y - 5 \) for \( y \). Plot the solution on a number line.
\( \displaystyle y = 8 \)

A horizontal number line from -1 to 10. The value 8 is plotted.]
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( 3 = y - 5 \) has subtraction on the same side of the equal sign as the variable. The inverse is addition. |
Step 2: Set up the inverse operation on both sides of the equation. |
Add 5 to both sides of the equation. \( \displaystyle 3 = y - 5 \) \( \displaystyle 3\bbox[yellow]{+ 5} = y - 5\bbox[yellow]{+ 5} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. \( \displaystyle 3\bbox[yellow]{+ 5} = y - 5\bbox[yellow]{+ 5} \) \( \displaystyle 8 = y - 5\bbox[yellow]{+ 5} \) Simplify the right-hand side of the equation. \( \displaystyle 8 = y - 5\bbox[yellow]{+ 5} \) \( \displaystyle 8 = y + 0 \) \( \displaystyle 8 = y \) |
Step 4: Check the solution using substitution. |
Substitute \( y = 8 \) into the original equation. Then simplify. \( \displaystyle 3 = \left( 8 \right) - 5 \) \( 3 = 3 \) |
Step 5: Plot the solution on a number line if requested. |
Plot a point that is 8 units to the right of 0. 
A horizontal number line from -1 to 10. The value 8 is plotted.] |
Solve the equation \( 3f = - 51 \) for \( f \). Plot the solution on a number line.
\( \displaystyle f = - 17 \)
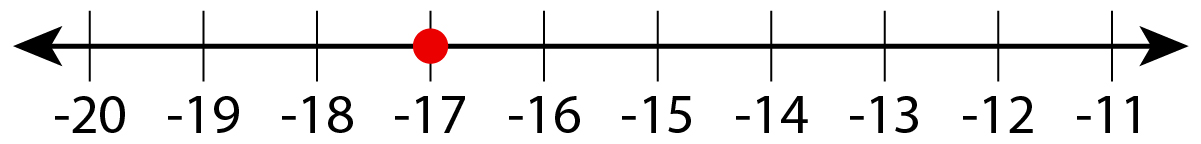
A horizontal number line from -20 to -11. The value -17 is plotted.]
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( 3f = - 51 \) has multiplication on the same side of the equal sign as the variable. The inverse is division. |
Step 2: Set up the inverse operation on both sides of the equation. |
Divide both sides of the equation by 3. \( \displaystyle 3f = - 51 \) \( \displaystyle \frac{3f}{\bbox[yellow]{3}} = \frac{- 51}{\bbox[yellow]{3}} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. Remember that the fraction bar indicates division, and any number divided by itself is 1. \( \displaystyle \frac{3f}{\bbox[yellow]{3}} = \frac{- 51}{\bbox[yellow]{3}} \) \( \displaystyle 1f = \frac{- 51}{\bbox[yellow]{3}} \) \( \displaystyle f = \frac{- 51}{\bbox[yellow]{3}} \) Simplify the right-hand side of the equation. \( \displaystyle f = \frac{- 51}{\bbox[yellow]{3}} \) \( \displaystyle f = - 17 \) |
Step 4: Check the solution using substitution. |
\( \displaystyle 3( - 17) = - 51 \) \( - 51 = - 51 \) |
Step 5: Plot the solution on a number line if requested. |
Plot a value 17 units to the left of 0. 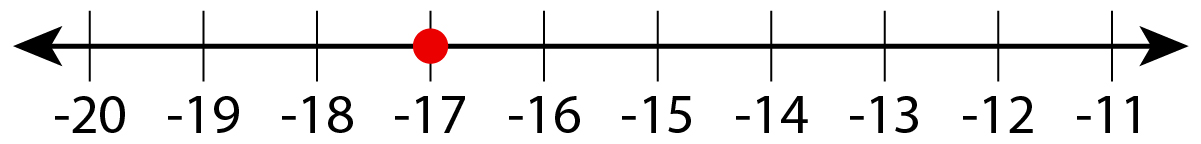
A horizontal number line from -20 to -11. The value -17 is plotted.] |
Willem's baseball league uses an average of 24 balls per game. Each team needs to provide a total of 720 new baseballs for the season.
The equation \( 24g = 720 \) represents this scenario, where \( g \) is the number of games each team in the league plays.

Solve the equation \( 24g = 720 \) for \( g \).
\( g = 30 \) games
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( 24g = 720 \) has multiplication on the same side of the equal sign as the variable. The inverse is division. |
Step 2: Set up the inverse operation on both sides of the equation. |
Divide both sides of the equation by 24. \( \displaystyle 24g = 720 \) \( \displaystyle \frac{24g}{\bbox[yellow]{24}} = \frac{720}{\bbox[yellow]{24}} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. \( \displaystyle \frac{24g}{\bbox[yellow]{24}} = \frac{720}{\bbox[yellow]{24}} \) \( \displaystyle 1g = \frac{720}{\bbox[yellow]{24}} \) \( \displaystyle g = \frac{720}{\bbox[yellow]{24}} \) Simplify the right-hand side of the equation. \( \displaystyle g = \frac{720}{\bbox[yellow]{24}} \) \( g = 30 \) games |
Step 4: Check the solution using substitution. |
Substitute \( g = 30 \) into the original equation. Then simplify. \( \displaystyle 24(30) = 720 \) \( 720 = 720 \) |
Step 5: Plot the solution on a number line if requested. |
This step was not requested. You can skip it for this problem. |
Solve \( \frac{4}{5} = x - \frac{1}{4} \) for \( x \). Plot the solution on a number line.
\( x = 1\frac{1}{20} \) or \( x = \frac{21}{20} \)
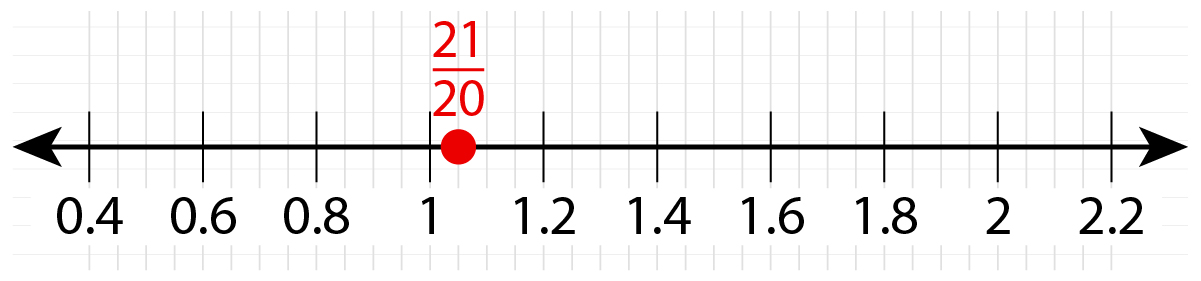
A horizontal number line from 0.4 to 2.2. The value \( \frac{21}{20} \) is plotted.]
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( \frac{4}{5} = x - \frac{1}{4} \) has subtraction on the same side of the equal sign as the variable. The inverse is addition. |
Step 2: Set up the inverse operation on both sides of the equation. |
Add \( \frac{1}{4} \) to both sides of the equation. \( \displaystyle \frac{4}{5} = x - \frac{1}{4} \) \( \displaystyle \frac{4}{5}\bbox[yellow]{+ \frac{1}{4}} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. Recall that you need common denominators to add fractions. The lowest common denominator (LCD) is 20. \( \displaystyle \frac{4}{5}\bbox[yellow]{+ \frac{1}{4}} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) \( \displaystyle \frac{4 \times 4}{5 \times 4}\bbox[yellow]{+ \frac{1 \times 5}{4 \times 5}} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) \( \displaystyle \frac{16}{20}\bbox[yellow]{+ \frac{5}{20}} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) \( \displaystyle \frac{21}{20} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) Simplify the right-hand side of the equation. \( \displaystyle \frac{21}{20} = x - \frac{1}{4}\bbox[yellow]{+ \frac{1}{4}} \) \( \displaystyle \frac{21}{20} = x - 0 \) \( \displaystyle \frac{21}{20} = x \) You can express \( \frac{21}{20} \) as \( 1\frac{1}{20} \) if you want to. |
Step 4: Check the solution using substitution. |
Substitute \( x = \frac{21}{20} \) into the original equation. Then simplify. Remember that you need common denominators to subtract fractions. \( \displaystyle \frac{4}{5} = \left( \frac{21}{20} \right) - \frac{1}{4} \) \( \displaystyle \frac{4}{5} = \frac{21}{20} - \frac{1 \times 5}{4 \times 5} \) \( \displaystyle \frac{4}{5} = \frac{21}{20} - \frac{5}{20} \) \( \displaystyle \frac{4}{5} = \frac{16}{20} \) Reduce the fraction on the right-hand side of the equation. \( \displaystyle \frac{4}{5} = \frac{16 \div 4}{20 \div 4} \) \( \displaystyle \frac{4}{5} = \frac{4}{5} \) |
Step 5: Plot the solution on a number line if requested. |
Plot a value that is \( \frac{21}{20} \) (or \( 1\frac{1}{20}) \) to the right of 0. 
A horizontal number line from 0.4 to 2.2. The value \( \frac{21}{20} \) is plotted.] |
Solve the equation \( 1.1h = 6.853. \) Plot the solution on a number line.
\( \displaystyle h = 6.23 \)

A horizontal number line from 6 to 6.45. The value 6.23 is plotted.]
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation on the variable in the equation. |
The equation \( 1.1h = 6.853 \) has multiplication on the same side of the equal sign as the variable. The inverse is division. |
Step 2: Perform the inverse operation on both sides of the equation. |
Divide both sides of the equation by 1.1. \( \displaystyle 1.1h = 6.853 \) \( \displaystyle \frac{1.1h}{\bbox[yellow]{1.1}} = \frac{6.853}{\bbox[yellow]{1.1}} \) |
Step 3: Simplify both sides of the equation. The variable should be isolated. When both sides are simplified, the equation is the solution. |
Simplify the left-hand side of the equation. \( \displaystyle \frac{1.1h}{\bbox[yellow]{1.1}} = \frac{6.853}{\bbox[yellow]{1.1}} \) \( \displaystyle 1h = \frac{6.853}{\bbox[yellow]{1.1}} \) \( \displaystyle h = \frac{6.853}{\bbox[yellow]{1.1}} \) Simplify the right-hand side of the equation. \( \displaystyle h = \frac{6.853}{\bbox[yellow]{1.1}} \) \( \displaystyle h = 6.853\bbox[yellow]{\div 1.1} \) \( \displaystyle h = 6.23 \) |
Step 4: Check the solution using substitution in the original equation. |
\( \displaystyle 1.1(6.23) = 6.853 \) \( 6.853 = 6.853 \) |
Step 5: Plot the solution on a number line if requested. |
Plot a value that is 6.23 units to the right of 0. 
A horizontal number line from 6 to 6.45. The value 6.23 is plotted.] |
Willem earns experience points (xp) for each level of a video game that he successfully completes. The game has 60 levels, and he can earn a maximum of 52 xp per level. The equation \( \frac{x}{60} = 52 \) represents this scenario.

Solve the equation \( \frac{x}{60} = 52 \) for \( x \), the maximum xp he can earn in the game.
\( x = 3,120 \) xp
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( \frac{x}{60} = 52 \) has division on the same side of the equal sign as the variable. The inverse is multiplication. |
Step 2: Set up the inverse operation on both sides of the equation. |
Multiply both sides of the equation by 60. \( \displaystyle \frac{x}{60} = 52 \) \( \displaystyle \frac{x}{60}\bbox[yellow]{\cdot 60} = 52\bbox[yellow]{\cdot 60} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. Remember that you can place any whole number over 1 to make it a fraction. \( \displaystyle \frac{x}{60}\bbox[yellow]{\cdot 60} = 52\bbox[yellow]{\cdot 60} \) \( \displaystyle \frac{x}{60}\bbox[yellow]{\cdot}\frac{\bbox[yellow]{60}}{1} = 52\bbox[yellow]{\cdot 60} \) \( \displaystyle \frac{\bbox[yellow]{60} x}{60} = 52\bbox[yellow]{\cdot 60} \) \( \displaystyle 1x = 52\bbox[yellow]{\cdot 60} \) \( \displaystyle x = 52\bbox[yellow]{\cdot 60} \) Simplify the right-hand side of the equation. \( \displaystyle x = 52\bbox[yellow]{\cdot 60} \) \( x = 3,120 \) xp |
Step 4: Check the solution using substitution. |
Substitute \( x = 3,120 \) into the original equation. Then simplify. \( \displaystyle \frac{(3,120)}{60} = 52 \) \( 52 = 52 \) |
Step 5: Plot the solution on a number line if requested. |
This step was not requested. You can skip it for this problem. |
Willem and six of his friends are going to see the new superhero movie! They are the first people to arrive at the show.
The equation \( s - 7 = 139 \) represents the number of seats remaining in the theater after Willem and his friends sit down. The variable \( s \) represents the total number of seats in the theater.

Solve the equation \( s - 7 = 139 \) for \( s \).
\( s = 146 \) seats
If you need help arriving at this answer, click the Solution button.
Step 1: Identify the inverse of the operation that is with the variable. |
The equation \( s - 7 = 139 \) has subtraction on the same side of the equal sign as the variable. The inverse is addition. |
Step 2: Set up the inverse operation on both sides of the equation. |
Add 7 to both sides of the equation. \( \displaystyle s - 7 = 139 \) \( \displaystyle s - 7\bbox[yellow]{+ 7} = 139\bbox[yellow]{+ 7} \) |
Step 3: Simplify both sides of the equation. |
Simplify the left-hand side of the equation. \( \displaystyle s - 7\bbox[yellow]{+ 7} = 139\bbox[yellow]{+ 7} \) \( \displaystyle s - 0 = 139\bbox[yellow]{+ 7} \) \( \displaystyle s = 139\bbox[yellow]{+ 7} \) Simplify the right-hand side of the equation. \( \displaystyle s = 139\bbox[yellow]{+ 7} \) \( s = 146 \) seats |
Step 4: Check the solution using substitution. |
Substitute \( s = 146 \) into the original equation. Then simplify. \( \displaystyle (146) - 7 = 139 \) \( 139 = 139 \) |
Step 5: Plot the solution on a number line if requested. |
This step was not requested. You can skip it for this problem. |
