Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each correct answer is correct—if you don't, review that part of the lesson.
The varsity volleyball team would like to raise at least $1,000. They begin selling posters for $10 and discount cards for $25. They would like to sell no less than 200 items. If \(p\) = the number of posters sold and \(d\) = the number of discount cards sold, then which system of linear inequalities represents this scenario?
-
\( 10d + 25p \geq 1000 \)
\( p + d \leq 200 \)
-
\( 10p + 25d \geq 1000 \)
\( p + d \geq 200 \)
-
\( 10d + 25p > 1000 \)
\( p + d \leq 200 \)
-
\( 25p + 10d \geq 200 \)
\( p + d < 1000 \)
Make sure that you match up the prices with the type of items sold and watch the direction of the inequality signs.
The phrases at least and no less than represent the inequality symbol \(\geq\). Write one inequality to represent the prices of the items in the fundraiser and another to represent the number of items the volleyball team would like to sell.
Pay close attention to the key phrase no less than. Which inequality symbol represents this phrase?
Make sure to match up the prices and goals with the type of item sold. Pay close attention to the direction of the inequality signs.
Which is NOT a system of linear inequalities?
-
\( y < x + 3 \)
\( y < - x + 3 \)
-
\( y \geq 2x + 2 \)
\( y \leq - x - 1 \)
-
\( y \geq x + 1 \)
\( y < 2n + 3 \)
-
\( 25p + 10d \geq 200 \)
\( p + d < 1000 \)
This is a system of linear inequalities because each inequality has the same variables and the power on the independent variable is one.
This is a system of linear inequalities because each inequality has the same variables and the power on the independent variable is one.
This is not a system of linear inequalities because the variables do not match. The first inequality has the variables \(x\) and \(y\) while the second has the variables \(n\) and \(y\).
This is a system of linear inequalities because each inequality has the same variables and the power on the independent variable is one.
If a graph contains an inequality represented by a dashed boundary line with shading below the line, which inequality symbol should you use?
- \(<\)
- \(>\)
- \(\leq\)
- \(\geq\)
Use this symbol when the boundary line is dashed and the shading is below the line.
Use this symbol when the boundary line is dashed and the shading is above the line.
Use this symbol when the boundary line is solid and the shading is below the line.
Use this symbol when the boundary line is solid and the shading is above the line.
In the graph shown, which is the equation of the green boundary line that slopes downward to the right?
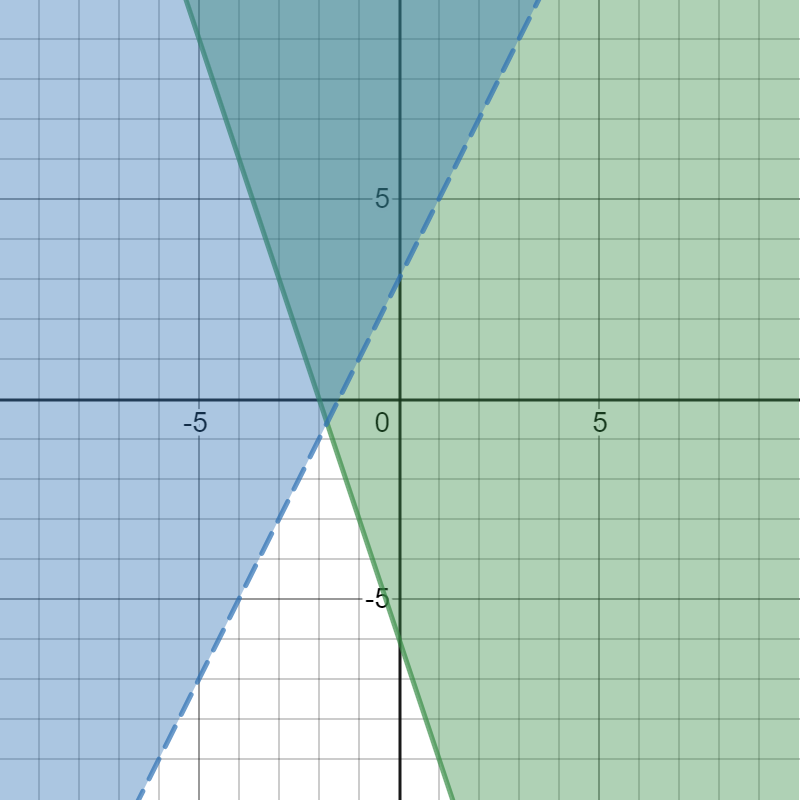
Two linear inequalities graphed on a coordinate plane where the shaded intersected regions are darker. The green graph has a solid line, a y-intercept of (0,-6), a slope of -3 and is shaded above the boundary line. The blue graph has a dashed line, a y-intercept of (0,3), a slope of 2 and is shaded above the boundary line.
- \(y = 2x + 3\)
- \(y > 2x + 3\)
- \(y < - 3x + 3\)
- \(y = - 3x - 6\)
This is the equation of the blue boundary line that slopes upward to the right.
This is the inequality represented by the blue boundary line.
You are looking for the equation of a boundary line. This equation will not include an inequality symbol.
Find the location of the \(y\)-intercept. It is \(\left( 0,\ - 6 \right)\text{. }\) Then, count along the line to calculate the slope. It is \(m = \frac{3}{- 1} = - 3\). The equation is \(y = - 3x - 6.\)
Which is the system of linear inequalities shown on this graph?
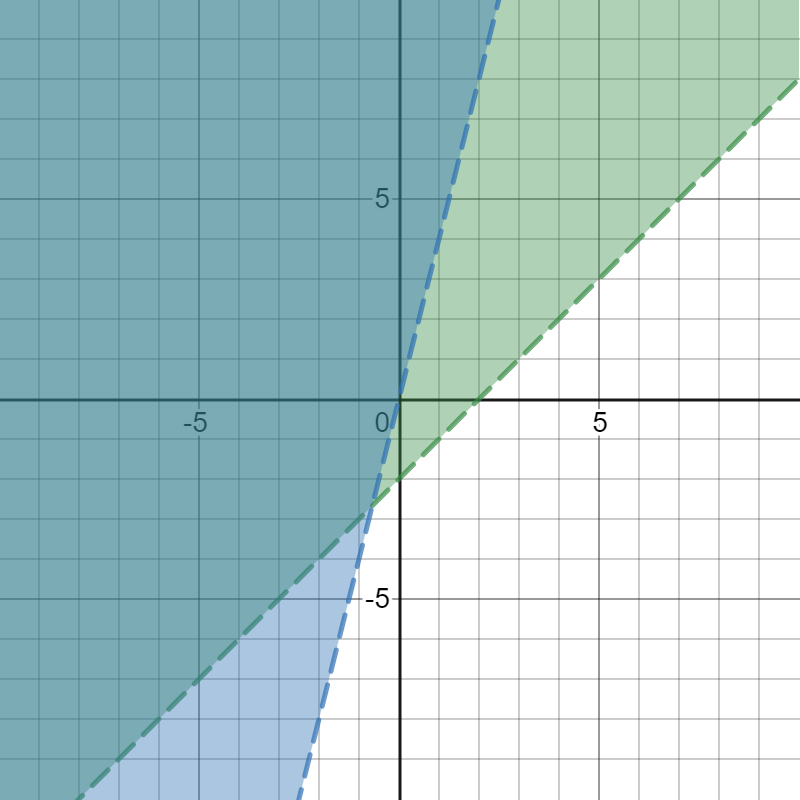
Two linear inequalities graphed on a coordinate plane where the shaded intersected regions are darker. One graph has a dashed line, a y-intercept of (0,0), a slope of 4 and is shaded above the boundary line. The other graph has a dashed line, a y-intercept of (0,-2), a slope of 1 and is shaded above the boundary line.
-
\( y > x - 2 \)
\( y > 4x \)
-
\( y > x - 2 \)
\( y \geq 4x \)
-
\( y > x - 2 \)
\( y > - 4x \)
-
\( y > - x - 2 \)
\( y > - 4x \)
Use what you know to write the equations of the boundary lines. They are \(y = x - 2\) and \(y = 4x\). Since both boundary lines are dashed and have shading above the line, use the symbol \(>\).
Both of the boundary lines on the graph are dashed, so both inequalities in this system should be strict inequalities.
Both of the boundary lines on the graph are positive. Recheck your slope calculations.
Both of the boundary lines on the graph are positive. Recheck your slope calculations.
Summary
Questions answered correctly:
Questions answered incorrectly:
