As you continue your studies of physics, you will need to create a way to keep track of all of your equations. You will reference them often and though it is not required that you memorize them, you likely will because you use them so often. You will be allowed to use a 3' x 5' note card with your equations on them for all your assessments. So far, you have learned two equations:
Displacement
\(\mathsf{\overrightarrow {d} = x_f - x_i = \Delta x}\)
where d is displacement and x is position.
Velocity
\(\mathsf{\overrightarrow {v} = \frac{x_f - x_i}{t_f - t_i} = \frac{\Delta x}{\Delta t}}\)
where x is position and t is time.
Work through these example problems to practice using the velocity equation to solve real-world problems.
Solve for v
Solve for d
Solve for t

If Harold ran +250. m in 30.0 seconds, what was his velocity?
| P |  |
| I | \(\mathsf{\Delta \overrightarrow {x} = +250. \text{ m} }\) \(\mathsf{\Delta t = 30.0 \text{ s} }\) \(\mathsf{\overrightarrow {v} = ? }\) |
| R | \(\mathsf{\overrightarrow {v} = \frac{\Delta x}{\Delta t} }\) |
| A | \(\mathsf{\overrightarrow {v} = \frac{+250. \text{ m}}{30.0 \text{ s}} }\) |
| T | \(\mathsf{\overrightarrow {v} = +8.33 \text{ m/s} }\) |
| E | He travelled with a velocity of +8.33 m/s. |
Janell ran a race with a average velocity of 16.5 km/hr. If she finished the race in 2.00 hours, how far was the race in kilometers?
| P | 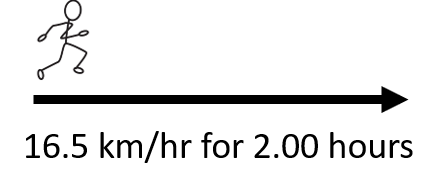 |
| I | \(\mathsf{\Delta \overrightarrow {x} = ? \text{ m} }\) \(\mathsf{\Delta t = 2.00 \text{ h} }\) \(\mathsf{\overrightarrow {v} = 16.5 \text{ km/hr} }\) |
| R | \(\mathsf{\overrightarrow {v} = \frac{\Delta x}{\Delta t} }\) \(\mathsf{\Delta x = \overrightarrow {v} \Delta t }\) |
| A | \(\mathsf{\Delta x = 16.5 \text{ km/hr} \cdot 2.00 \text{ hr} }\) |
| T | \(\mathsf{\Delta x = 33.0 \text{ km} }\) |
| E | The race was 33.0 kilometers in distance. |

How long will it take Joshua to walk from his house to the local ice cream shop, a distance of 402 meters, if his average speed is 1.55 m/s?
| P | 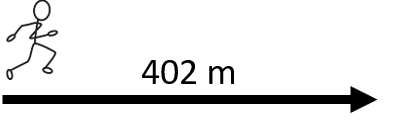 |
| I | \(\mathsf{\Delta \overrightarrow {x} = 402 \text{ m} }\) \(\mathsf{\Delta t = ? \text{ h} }\) \(\mathsf{\overrightarrow {v} = 1.55 \text{ m/s} }\) |
| R | \(\mathsf{\overrightarrow {v} = \frac{\Delta x}{\Delta t} }\) \(\mathsf{\Delta t = \frac{\Delta x}{\overrightarrow {v}} }\) |
| A | \(\mathsf{\Delta t = \frac{402 \text{ m}}{1.55 \text{ m/s} } }\) |
| T | \(\mathsf{\Delta t = 259. \text{ s} }\) |
| E | It took Joshua 259 seconds (or 4.32 minutes) to walk to the ice cream shop. |
