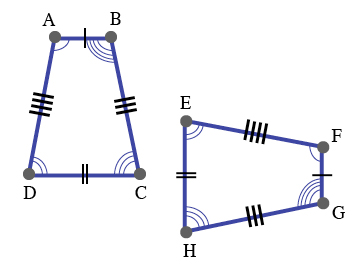
Look closely at the two trapezoids on the right, which we'll name ABCD and EFGH. As we just learned, these two shapes are congruent if their sizes and shapes are identical.
Question
To demonstrate that trapezoid ABCD and trapezoid EFGH are identical, what things might we need to show?
that the corresponding angles are identical and that the corresponding sides are identical in measurement
Of course, the first thing we need to do is to determine what the corresponding sides and angles are. The easiest way to figure out corresponding sides and angles is to arrange the images side by side so they appear to "sit" the same, as shown below.

In this example, we can say that ABCD and FGHE are congruent because their sides and angles are the same. In mathematical terms, we would write ABCD \(\small\mathsf{ \cong{} }\)FGHE, which means "ABCD is congruent to FGHE."
Did you notice that the number of pencil marks (called ticks) match up in both shapes? These marks indicate congruence--the sides that have one tick mark are congruent, the sides that have two tick marks are congruent, and so on. To show that angles are congruent, we use one angle marking for the first pair of congruent angles, two angle markings for the second pair, and so on.
Try It!
Can you state in mathematical terms which sides and angles in trapezoids ABCD and EFGH are congruent?
The congruent sides are \(\small\mathsf{ \overline{AB} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \overline{FG} }\), \(\small\mathsf{ \overline{AD} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \overline{FE} }\), \(\small\mathsf{ \overline{BC} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \overline{GH} }\), and \(\small\mathsf{ \overline{DC} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \overline{EH} }\).
The congruent angles are \(\small\mathsf{ \angle{A} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{F} }\), \(\small\mathsf{ \angle{C} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{H} }\), \(\small\mathsf{ \angle{B} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{G} }\), and \(\small\mathsf{ \angle{D} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{E} }\).
