Model Zoo
Create models to represent the fractions in the word problems.
Goal:
Goal:
 The local zoo is doing a bit of remodeling. They need to divide
some of their animal pens to accommodate some new animals. The
zookeepers are making a plan to show the construction crew what
they need. Use what you know about fraction models and division
to create models the zookeepers can use to show their plans.
The local zoo is doing a bit of remodeling. They need to divide
some of their animal pens to accommodate some new animals. The
zookeepers are making a plan to show the construction crew what
they need. Use what you know about fraction models and division
to create models the zookeepers can use to show their plans.
Here is an example to help you.
Currently, the elephants share 2 large pens. The zoo needs to divide the 2 original pens to make 4 new pens total. How much space will each new pen receive? This problem can be represented by the division expression 2 ÷ 4. As a model, that would look like:

Two spaces divided into four sections, 2 ÷ 4. As you can see with the model, each new pen will be \(\mathsf{ \frac{1}{2} }\) of an original pen.
So, \(\mathsf{ 2 \div 4 = \frac{1}{2} }\).
For each problem below, write a division expression, and create a model that represents the problem.
This problem can be represented by the division expression 4 ÷ 6. The 4 original pens are being divided into 6 new pens total. As a model, that would look like this:
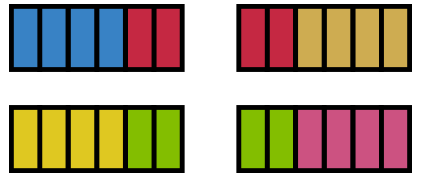
The 6 colors represent the 6 groups (new pens). Each new pen will be \(\mathsf{ \frac{4}{6} }\) of the old pens: \(\mathsf{ 4 \div 6 = \frac{4}{6} }\).
This problem can be represented by the division expression 1 ÷ 3. The 1 original lion pen is being divided into 3 new pens. The model representing this scenario would look like this:

The 3 colors represent the 3 groups (new pens). Each new pen will be \(\mathsf{ \frac{1}{3} }\) of the old pen: \( 1 \div 3 = \mathsf{ \frac{1}{3} }\).
This problem can be represented by the division expression 5 ÷ 8. The 5 original giraffe stalls are being divided into 8 stalls. This is represented in the model below:
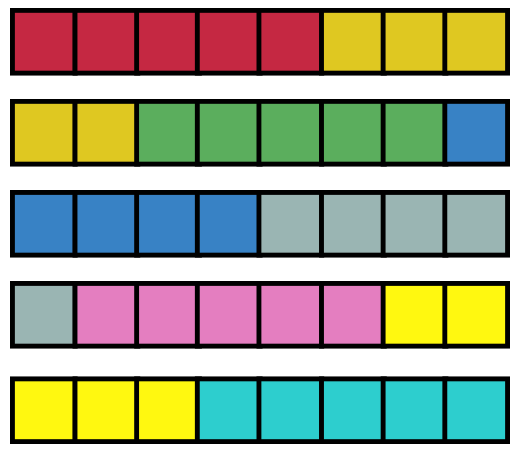
The 8 colors represent the 8 groups, or stalls. Each new stall will be \(\mathsf{ \frac{5}{8} }\) of the old pens: \(\mathsf{ 5 \div 8 = \frac{5}{8} }\) .