Problem Solving
Solve problems related to the total area of rectangular figures.
Goal:
Goal:

Practice!
Goal: Check your understanding of area and using decomposition to find the total area.
Remember, when you are finding the total area of something, you find the area of each section, then add the different areas together.
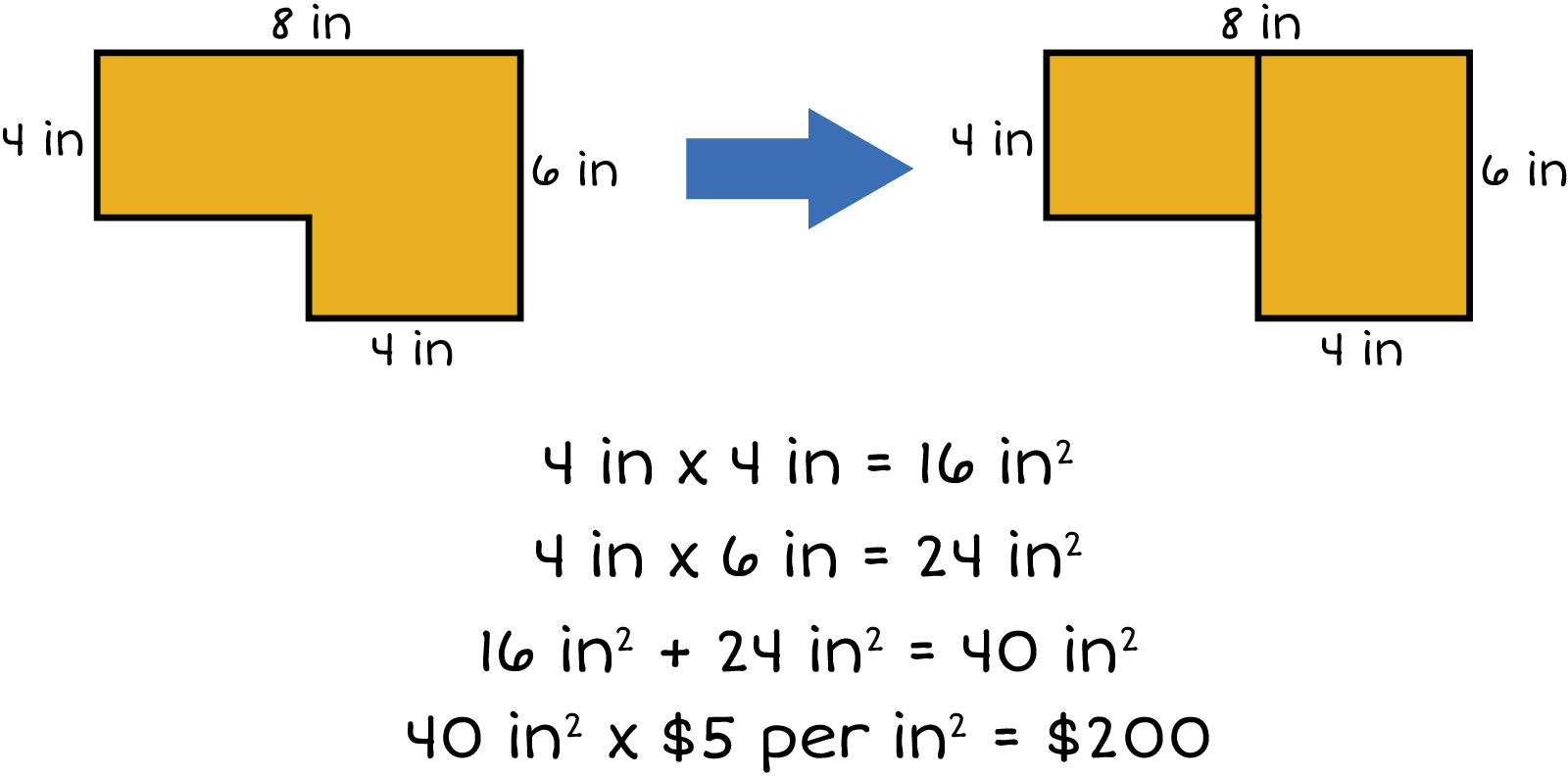
An area of with the left width 4 inches wide, top length 8 inches, right width 6 inches and bottom length of the right section is 4 inches. An arrow points to the same area now divided into two sections with veritcally. The first section now is 4 inches wide and 4 inches in length. The second section is now 6 inches in width and 4 inches in length. The decomposition equations are 4 inches times 4 inches equals 16 inches squared. 4 inches times 6 inches equals 24 inches squared. 16 inches squared plus 24 inches squared equals 40 inches squared. 40 inches squared times 5 dollars per inches squared equals 200 dollars.
Let’s practice finding the total area and cost of rectangular figures. Remember to use these problem-solving steps to help you find the answers to word problems.
Word Problem Solving Steps
- Read the problem.
- Look for important information.
- Write a math sentence.
- Choose a way to solve.
- Solve and label your answer.

Solve for the total area and cost using decomposition.
Rick is putting a porch around the side of his house and needs to find the total area that the porch will cover. What is the area of the porch? If the materials are $3 per square foot, what is the total cost?
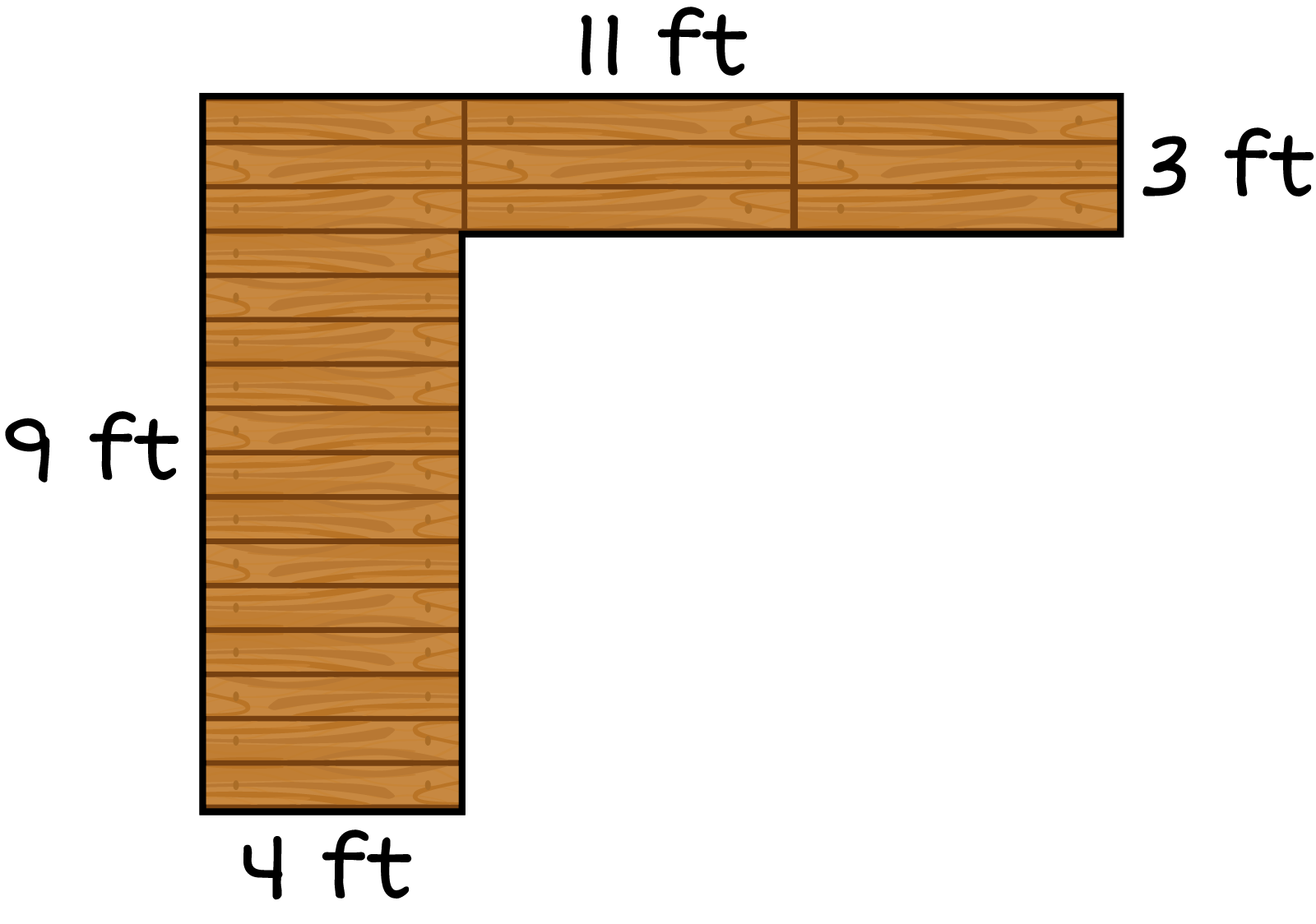
Total Cost of Materials \({=}\) $
That’s right, Area of left side is 9 feet \({\times}\) 4 feet \({=}\) 36 ft\({^2}\), Area of front is 7 feet \({\times}\) 3 feet \({=}\) 21 ft\({^2}\), Total area of porch is 36 ft\({^2}\) \({+}\) 21 ft\({^2}\) \({=}\) 57 ft\({^2}\); Total Cost of Materials: 57 ft\({^2}\) \({\times}\) $3 \({=}\) $171.
That’s incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together. Multiply the total area times the unit cost.
Solve for the total area.
Michael is going to be taking a trip with his family. His bag is 4 units by 6 units, and his brother’s bag is 3 units by 8 units. What is the area of Michael’s bag? What is the total area of both bags?

Total Area of both bags \({=}\) square units
That’s right, Area of the Michael’s bag is 4 units \({\times}\) 6 units \({=}\) 24 square units, and his brother’s bag is 3 units \({\times}\) 8 units \({=}\) 24 square units, Total area of both bags is 24 square units \({+}\) 24 square units \({=}\) 48 square units
That’s incorrect. Find the area of each bag, and finally add the different areas together. Area is length times width.
Solve for the total cost and area using decomposition.
Lily is building an enclosure for her chickens. She needs to cover the bottom in sawdust, which costs $6 per square foot. What is the total area that needs to be covered and the total cost of sawdust?

Total cost of sawdust \({=}\) $ ft\({^2}\)
That’s right, Area of the enclosure can be broken into two sections one is 4 feet \({\times}\) 6 feet \({=}\) 24 ft\({^2}\), and the other is 2 feet \({\times}\) 3 feet \({=}\) 6 ft\({^2}\), Total area of the enclosure is 24 ft\({^2}\) \({+}\) 6 ft\({^2}\) \({=}\) 30 ft\({^2}\), Total cost is 30ft\({^2}\) \({\times}\) $6 per ft\({^2}\) \({=}\) $180.
That’s incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together. To find the cost, multiply the total area by the unit cost.
Solve for the total area using decomposition.
Desmond has a corner desk in his bedroom and wants to put a new tabletop on it. What is the area of the tabletop that he needs to buy? If the materials are $3 per square unit, what is the cost of the new tabletop?

Total cost of tabletop: \({=}\) $
That’s right, Area of one section is 2 units \({\times}\) 10 units \({=}\) 20 square units, Area of the other section is 9 units \({\times}\) 3 units \({=}\) 27 square units, Total area of the tabletop is 20 square units \({+}\) 27 square units \({=}\) 47 square units.
That’s incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together.
Solve for the total area using the distributive property.
Frazer is trying to make some extra money in the summer. He decides to mow lawns in his neighborhood. He mows two lawns next to one another, one that is 3 meters by 9 meters and the other that is 3 meters by 4 meters. What is the total area that he mows? If he charges $2 per square meter, how much does he make?
Total amount collected \({=}\) $
That’s right, Area of the first lawn is 3 meters \({\times}\) 9 meters \({=}\) 27 square meters, Area of the second lawn is 3 meters \({\times}\) 4 meters \({=}\) 12 square meters, Total area of the two lawns is 27 square meters \({+}\) 12 square meters \({=}\) 39 square meters; 39 square meters \({\times}\) $2 per square meter \({=}\) $78
That’s incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together. Multiply the total area by the unit cost.
Great Job!