Assess Yourself
How well do you understand the ideas in this lesson?
Goal:
Goal:

Show What You Know!
Are you ready to take this lesson's quiz? These questions will help you find out. Go back to the lesson if you do not know an answer.
Find the total cost.
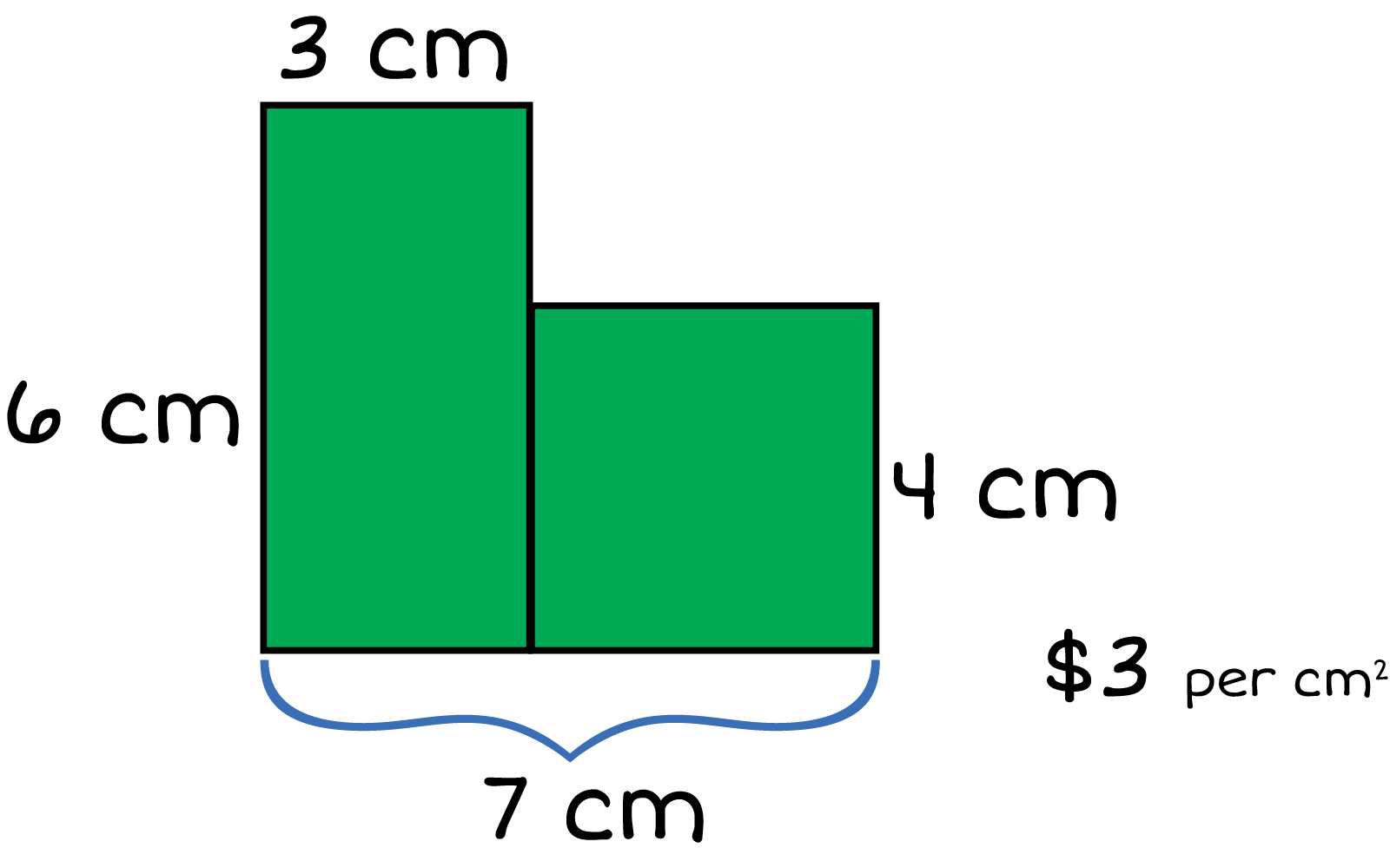
An area with two sections. The left width is 6 centimeters. The top lenght is 3 centimeters. The second section right width is 4 centimeters and the total bottom length is 7 centimeters.
- $102
- $126
- $34
- $48
This is correct! 6 cm \({\times}\) 3 in \({=}\) 18 cm \({^2}\), 4 cm \({\times}\) 4 cm \({=}\) 16 cm\({^2}\), 18 cm\({^2}\) \({+}\) 16 cm\({^2}\) \({=}\) 34 \({^2}\) \({\times}\) $3 per cm\({^2}\) \({=}\) $102
This is incorrect. It looks like you found the area for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area.
This is incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together.
This is incorrect. It looks like you added all the measurements, instead of breaking the shape into smaller rectangles, finding the areas of each part, and then adding to get the total area.
Find the total area:
An grid with two sections. The first width is 8 units and a length of 2 units. The second section with is 3 units the length is 6 units.
- 34 square units
- 16 square units
- 18 square units
- 42 square units
Great job! \({(2 \times 8) + (6 \times 3) = 16 + 18 = 34}\) square units
This incorrect. It looks like you found the area for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area.
This is incorrect. It looks like you found the area for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area.
This incorrect. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together.
What is the total area?

A grid that is made up of two sections the frist section is 10 units in width and 2 units in length the second section is 8 units wide and 2 units in lenght.
- 36 square units
- 100 square units
- 20 square units
- 24 square units
This is correct! \({(2 \times 10) + (8 \times 2) = 20 + 16 = 36}\) square units
This is incorrect. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together.
Try again. It looks like you found the area for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area.
Try again. It looks like you added all of the measurements instead of breaking the shape into smaller rectangles, finding the areas of each part, and then adding to get the total area.
Find the total cost.

An area the left width is 8 inches, the top lenght is 10 inches, the right width is 3 inches the bottom length is 5 inches. The cost is 8 dollars per square inch.
- $440
- $640
- $55
- $320
Great job! \({(5 \times 5) + (10 \times 3) = 25 + 30 = 55 \text{ in}^2}\) or \({(5 \times 8) + (5 \times 3) = 40 + 15 = 55\text{ in}^2 \times $8 = $440}\)
Try again. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together. Then, multiply the area by the unit cost.
Try again. Make sure you are multiplying the total area by the unit cost to find the total cost.
Try again. It looks like you found the cost for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area, which is then multiplied by the unit cost.
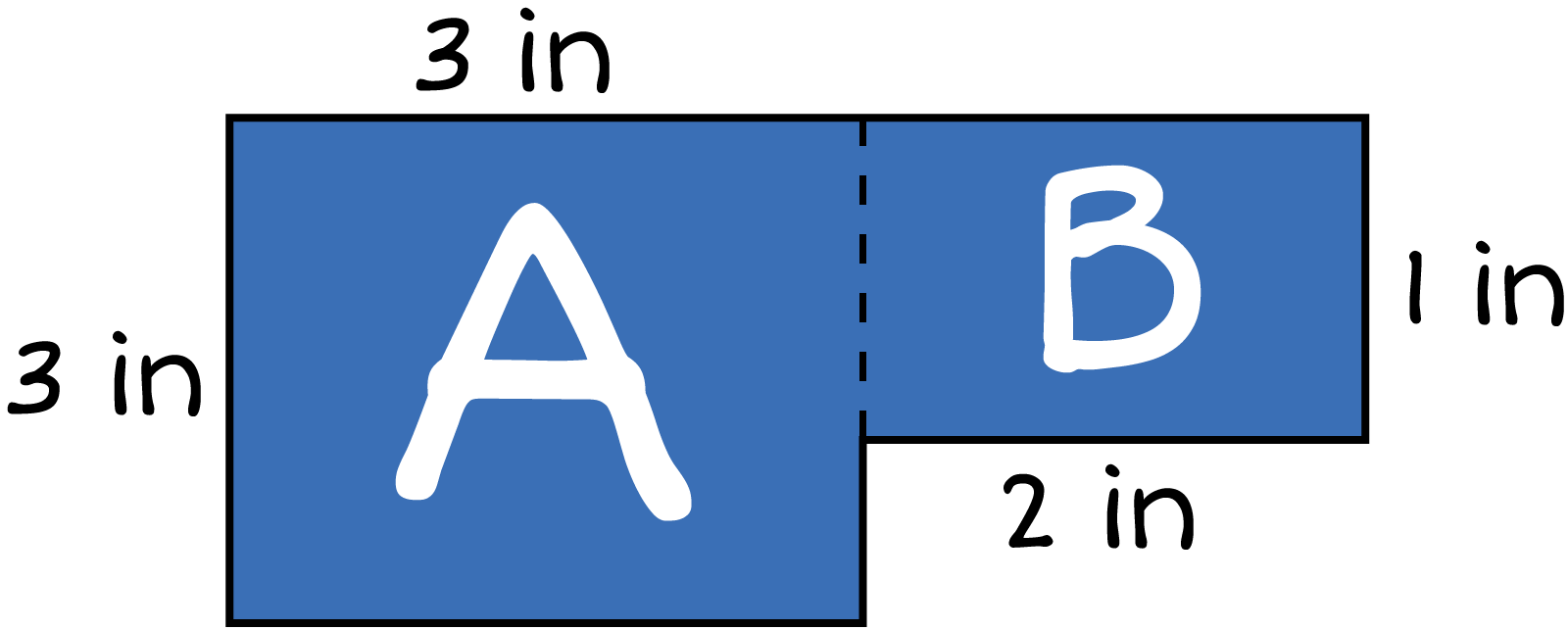
In which line did the FIRST mistake occur?

An area with two sections section A: width 3 inches and top length of 3 inches. Section B: has a width 1 inch and a bottom length of 2 inches. Line 1: Area of part \({A = 3 \text{ in} \times 3\text{ in} = 9 \text{ in}^2}\) Line 2: Area of part \({B = 2\text{ in} \times 1\text{ in} = 3\text{ in}^2}\) Line 3: \({9\text{ in}^2 + 3\text{ in}^2}\) Line 4: \({12 \text{ in}^2}\)
- Line 1
- Line 2
- Line 3
- Line 4
That is incorrect. This is the correct value for the area of part A.
Correct! This is the first error. This is the incorrect value for the area of part B. It should be: \({2\text{ in} \times 1\text{ in} = 2\text{ in}^2}\).
This is incorrect. This is the correct action to take at this step to find the total area, even if the values are incorrect.
This is incorrect. This is the sum of the areas found for this figure. 9 in\({^2}\) and 3 in\({^2}\) are not the correct areas of the separate parts.
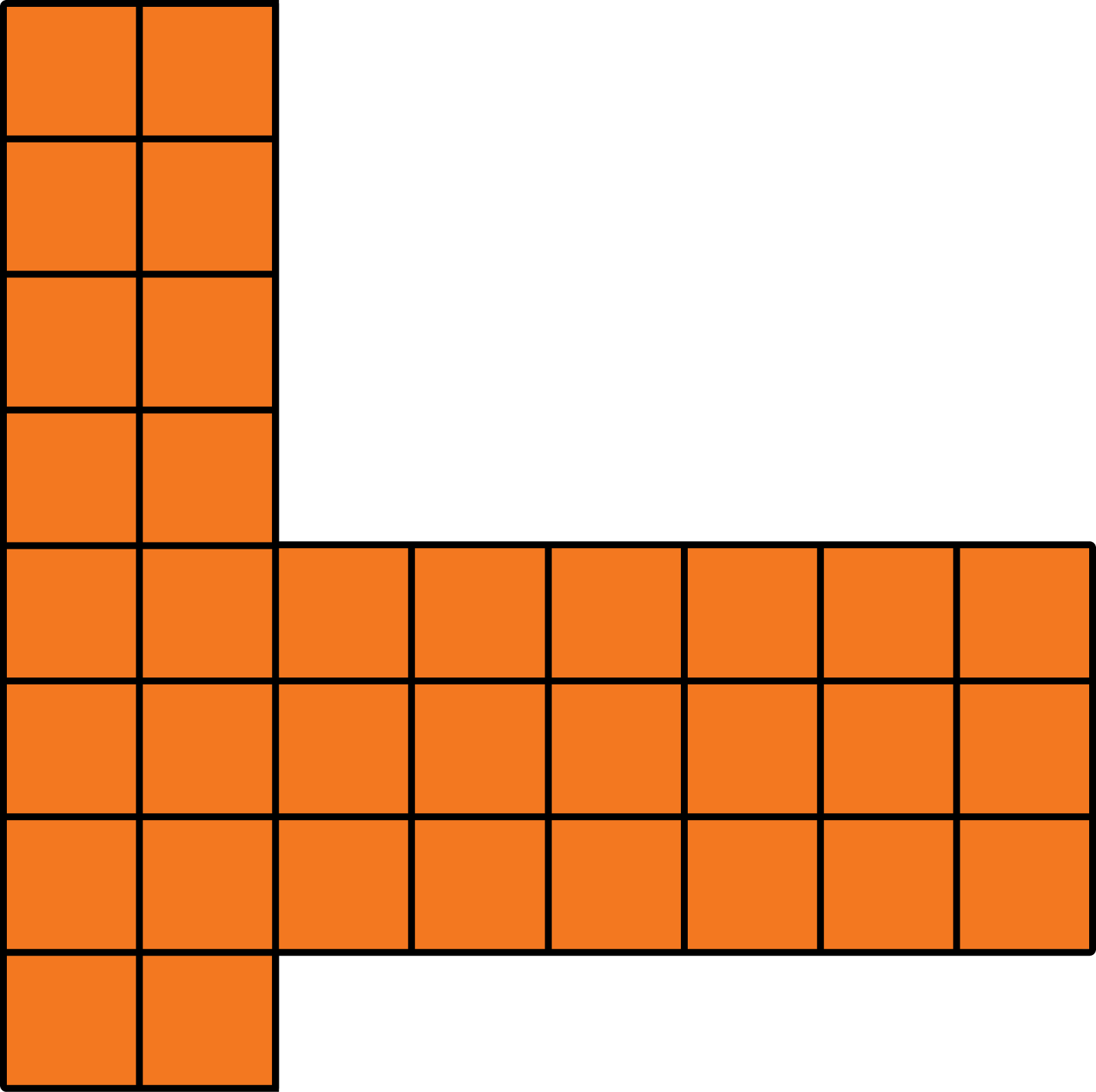
Find the total area.
An area made of two parts A: width: 3 inches, lenght: 3 inches. B: width:1 inches, length 2 inches
- 11 in\({^2}\)
- 12 in\({^2}\)
- 9 in\({^2}\)
- 15 in\({^2}\)
That is correct.
Try again. Check your calculations of the area of each part.
Try again. It looks like you found the area for one of the parts. Remember to find the area of both parts and then add them to get the total area.
Try again. It looks like you multiplied the sides together and added them. Remember, you MUST break the figure into smaller rectangular shapes first, find the area of each section, and finally add the different areas together.
Find the total cost.

An area. The left width is 9 inches, the top right lenght is 3 inches, the rigth width is 7 inches and the bottom length is 10 in. The const is 4 dollars per square inch.
- $360
- $336
- $280
- $400
Try again. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together. Then, multiply by the unit cost.
Great job! \({(10 \times 7) + (7 \times 2) = 70 + 14 = 84\text{ in}^2}\) or \({(9 \times 7) + (3 \times 7) = 63 + 21 = 84\text{ in}^2 \times $4 = $336}\)
Try again. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together. What are the measurements of the different sections?
Try again. It looks like you multiplied the sides together and added them. Remember, you MUST break the figure into smaller rectangular shapes first, find the area of each section, and finally add the different areas together. Then, multiply by the unit cost.
Finn has a vegetable garden in his backyard and needs to buy some soil to add for this spring season. The garden has two portions. Tomatoes grow in a portion that is 4 meters by 5 meters, and peppers grow in a portion that is 3 meters by 3 meters. If the soil costs $5 per square meter, how much will it cost to cover both portions?
- $100
- $45
- $145
- $29
This is incorrect. Remember to break the figure into smaller rectangular shapes, then find the area of each section, and finally add the different areas together. Then, multiply by the unit cost.
This is incorrect. It looks like you found the area for one of the parts. Remember, you need to find the area of both parts and then add them to get the total area. Then, multiply by the unit cost.
Great job! \({(4 \times 5) + (3 \times 3) = 20 + 9 = 29\text{ m}^2 \times $5 = $145}\)
This is incorrect. This question is asking to find the total cost. You have found the total area.
Nelson is painting two walls in his room. One wall is 8 feet high and 12 feet wide, the other is 8 feet high and 10 feet wide. If the cost of paint is $10 per square foot, what will it cost to paint both walls?
- $1760
- $800
- $960
- $176
That is correct. \({(8 \times 12) + (8 \times 10) = 96 + 80 = 176 \text{ ft}^2 \times $10 = $1760}\)
This is incorrect. Remember to add both sections together to find the total area. Then, multiply by the unit cost.
That is incorrect. Remember to add both sections together to find the total area. Then, multiply by the unit cost.
This is incorrect. To find the total cost, you must multiply the total area by the unit cost, $10 per square foot.
Find the total cost.
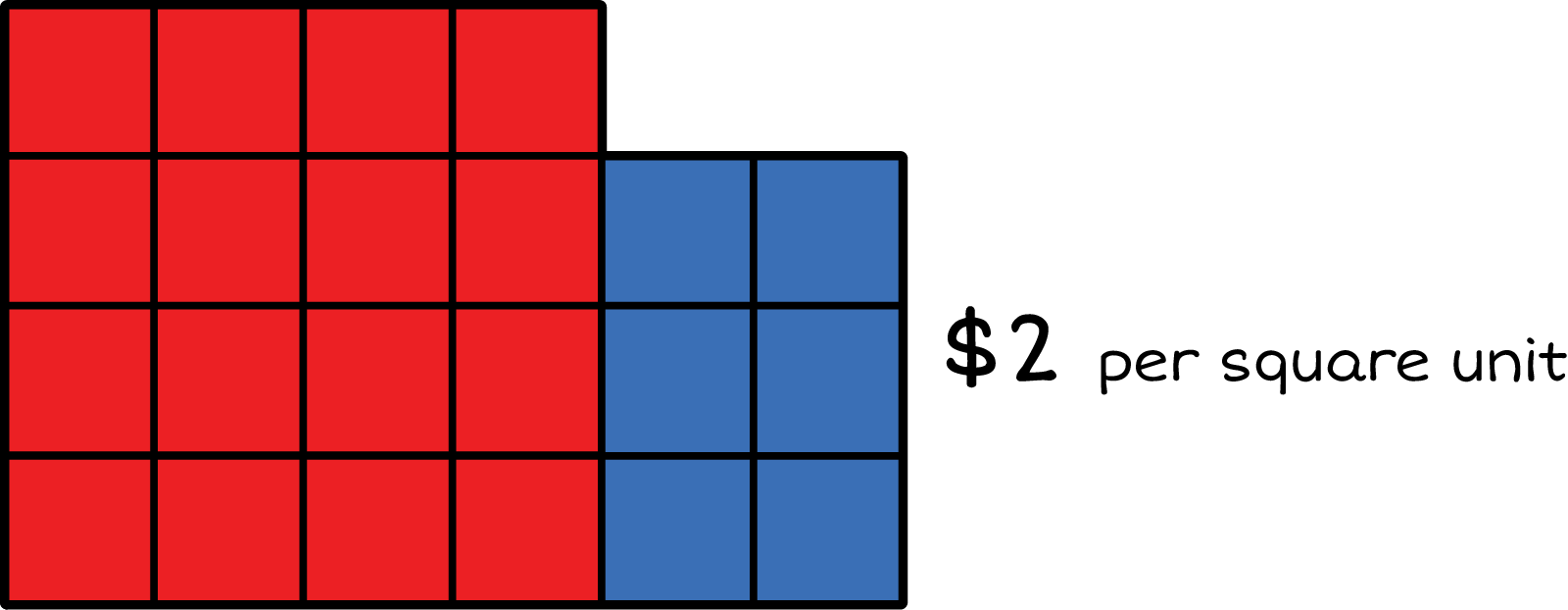
A grid made of two sections the first section is 4 units wide and 4 units in length. The second section is 3 units wide and 2 units in lenght.
- $44
- $48
- $32
- $12
This is correct! \({(4 \times 4) + (2 \times 3) = 16 + 6 = 22}\) square units \({\times}\) $2 per square unit \({=}\) $44
This is incorrect. Remember to break the figure into smaller rectangular shapes, find the area of each section, and finally add the different areas together. Then, multiply by the unit cost.
This is incorrect. Remember to add the different areas together. Then, multiply by the unit cost.
This is incorrect. Remember to add both sections together. Then, multiply by the unit cost.
Summary
Questions answered correctly:
Questions answered incorrectly: