Let’s Learn!
What strategies can I use to solve problems related to finding the area?
Goal:
Goal:

Think About It!
Goal: Analyze and solve area word problems by decomposing a rectangle.
Airports have many departments that are responsible for different jobs. We will find the area and cost of the departments that are going to be in the new airport. But first we need to review the steps to finding the area and total cost.
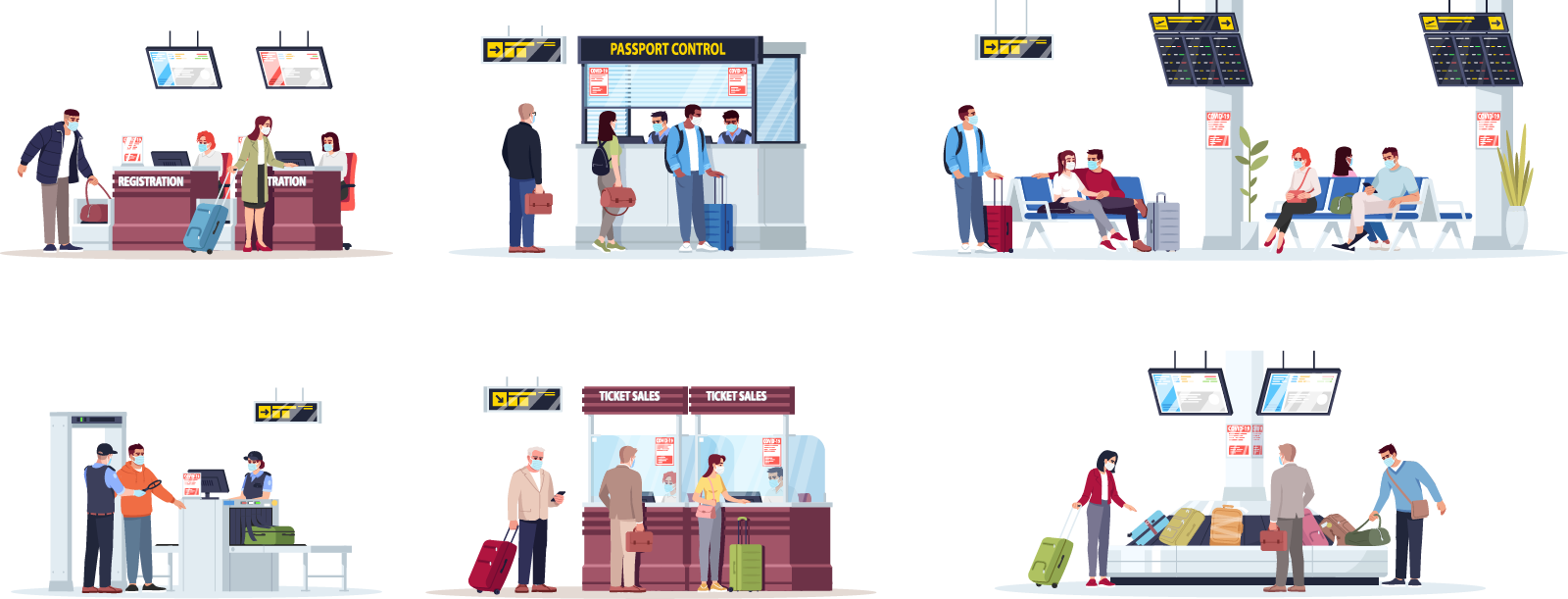
Many different areas of the Airport where people work. There is a registration area, a passport area, a terminal area, a security area, a tickets sales area and a baggage pick up area. All these areas require different amount of space.
Let’s review the different strategies that are needed to solve problems about total area and cost.
Click on the strategies below to see how to find the area of rectangular shapes.
Area is the measurement of space in a shape. The area of a rectilinear shape is found by multiplying the shape’s length and width.
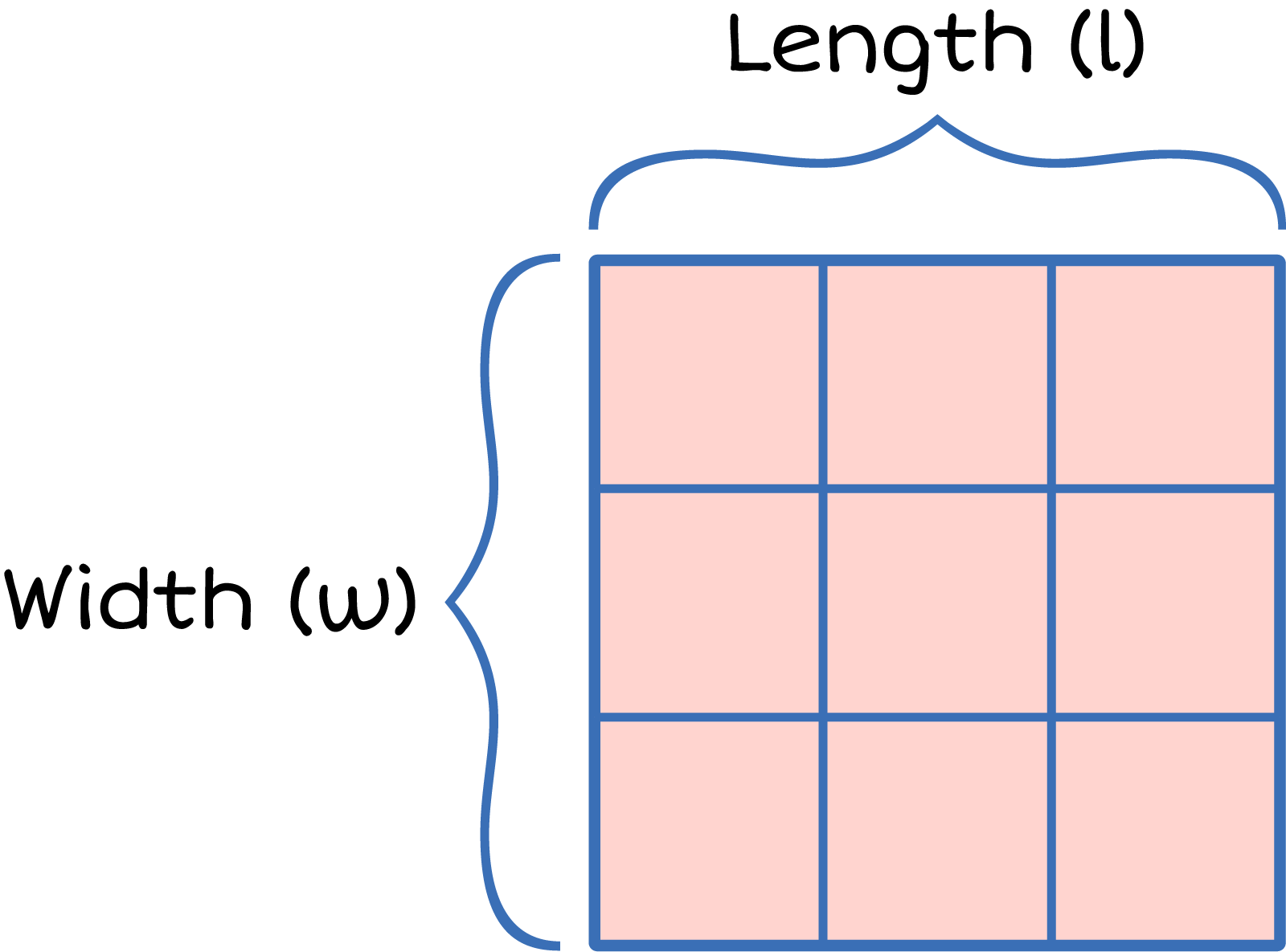
An area that is 3 in width and 3 units in length. The width is marked with Width (w) and length is marked with length (l)
Area \({= l \times w}\)
Area \({=}\) 3 units \({\times}\) 3 units \({=}\) 9 units.
We can use the distributive property to solve problems when we have a shape like the one below. The distributive property says that multiplying a sum by a number is the same as multiplying each addend by that number and then adding the product. Try it, then click on the Show Me button to check your answer.
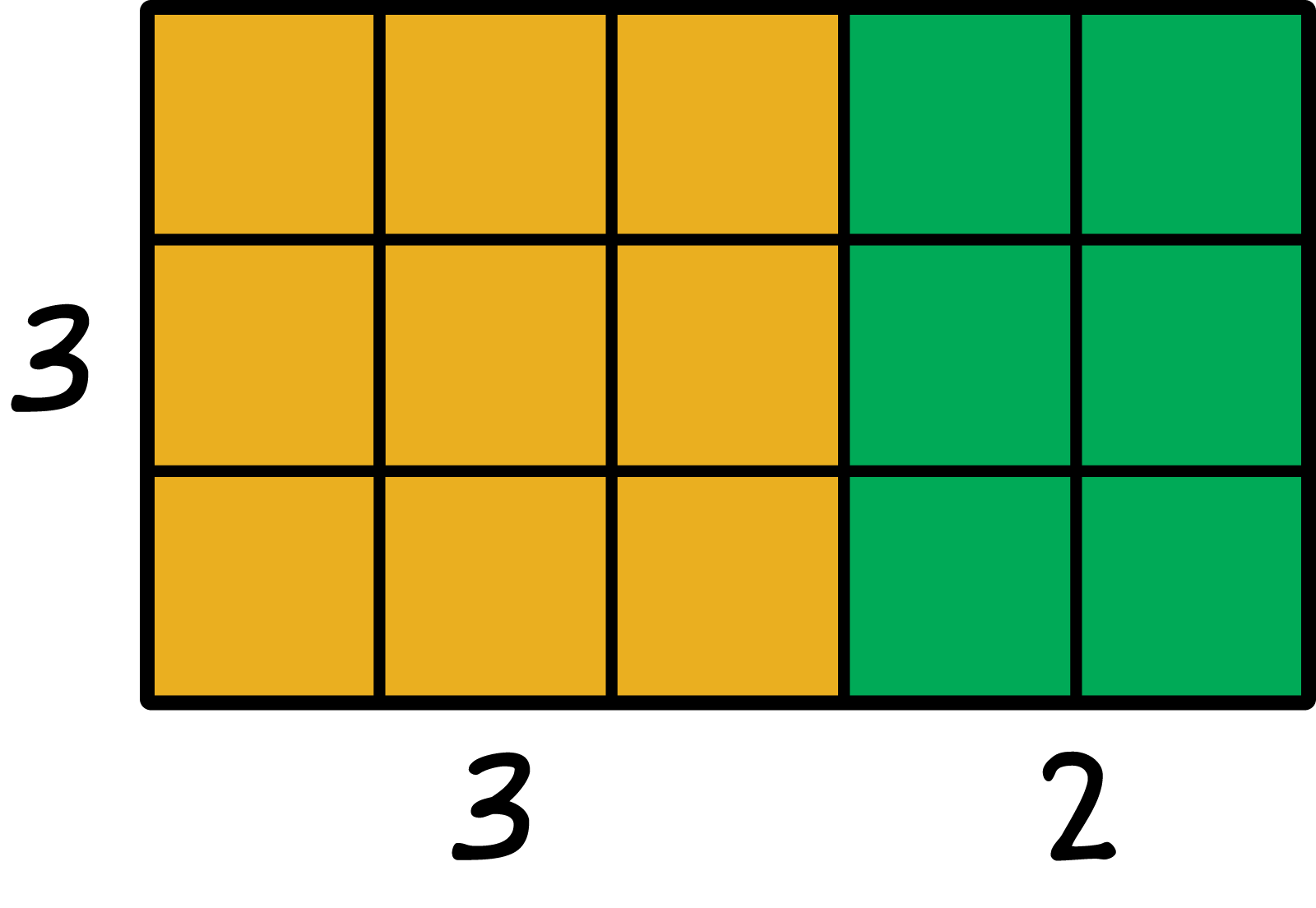
A grid with a length of 5 and a width of 3. The grid is broken into two sections the first is a 3 wide and 3 in lenght and the second is 3 wide and 2 length.
\({3 \times (3 + 2) = (3 \times 3) + (3 \times 2)}\)
9 square units \({+}\) 6 square units \({=}\) 15 square units.
What do you do when you have a shape like the one below that has different areas of rectangular shapes? You decompose, or break, the shape into smaller shapes.

An area. The left width is 8 centimeters, the right length is 10 centimeters, the right width is 12 centimeters and the bottom length is 15 centimeters.
The example above can be separated into two rectangular shapes.
We know that the length of one section is 10 centimeters, and the total measure of its opposite side is 15 centimeters. So, we can determine that the length of the smaller section is 5 centimeters.

An area. The left width is 8 centimeters, the right length is 10 centimeters, the right width is 12 centimeters. The left bottom is 5 centimeters and the right bottom is 10 centimeters. Adding the bottom lengths together is 15 centimeters.
Using our new measurements, we can calculate the area of each section and the total area. Try it! Then, click on the Show Me button to check your work.
\({8 \text{ cm} \times 5 \text{ cm} = 40 \text{ cm}^2}\)
\({12 \text{ cm} \times 10 \text{ cm} = 120 \text{ cm}^2}\)
\({40 \text{ cm}^2 + 120 \text{ cm}^2 = 160 \text{ cm}^2}\)
The total area is 160 cm\({^2}\)
Once you have found the total area of a shape, you can use the unit cost to find the total cost of something.
Let’s take our previous shape:

An area. The left width is 8 centimeters, the right length is 10 centimeters, the right width is 12 centimeters and the bottom length is 15 centimeters.
\({8 \text{ cm} \times 5 \text{ cm} = 40 \text{ cm}^2}\)
\({12 \text{ cm} \times 10 \text{ cm} = 120 \text{ cm}^2}\)
\({40 \text{ cm}^2 + 120 \text{ cm}^2 = 160 \text{ cm}^2}\)
If the cost per square centimeter was $2, what would be the total cost? click on the Show Me button to see the total cost.
Total Area \({\times}\) cost per square unit \({=}\) Total cost of area.
\({160 \text{ cm}^2 \times $2\text{ per cm}^2 = $320}\)
The total cost of this shape is $320.
Let’s see if we can help calculate the total areas and costs of the different departments of the new airport.