Let’s Learn!
How can you multiply to find the area?
Goal:
Goal:

Think About It!
Goal: Calculate the area of a rectangle by using repeated addition and multiplication.
Area is the number of square units needed to cover a flat surface. Knowing how to find the area of something is important in everyday life. Maybe you want to know how much paint you need to paint the walls of a room. Maybe a landscaper needs to measure the area of a yard to know how much to charge to cut the grass. When you play a sport, the field should be a specific area.
Let's look at several ways to calculate area. Different units of measurement can be used such as centimeters (cm), inches (in.), feet (ft), or meters (m). Area is labeled as square units: square cm, square in., square ft, or square m. We can also label area using a shortcut. If we want to show 30 square centimeters, we can write 30 cm2! That little 2 means squared!
Click on each row to learn ways for measuring the area of a rectangle.
Remember, one way to measure the area of a shape is to tile it, or create a grid and count each tile or square unit. There are 9 tiles. Each tile is a square, so the measurement is in square units.
The area of this rectangle is 9 square units.

Another way to write that is 9 units\({\Large^2}\)!
We can also find area using repeated addition. When using repeated addition, you look at the number of rows and the number in each row.
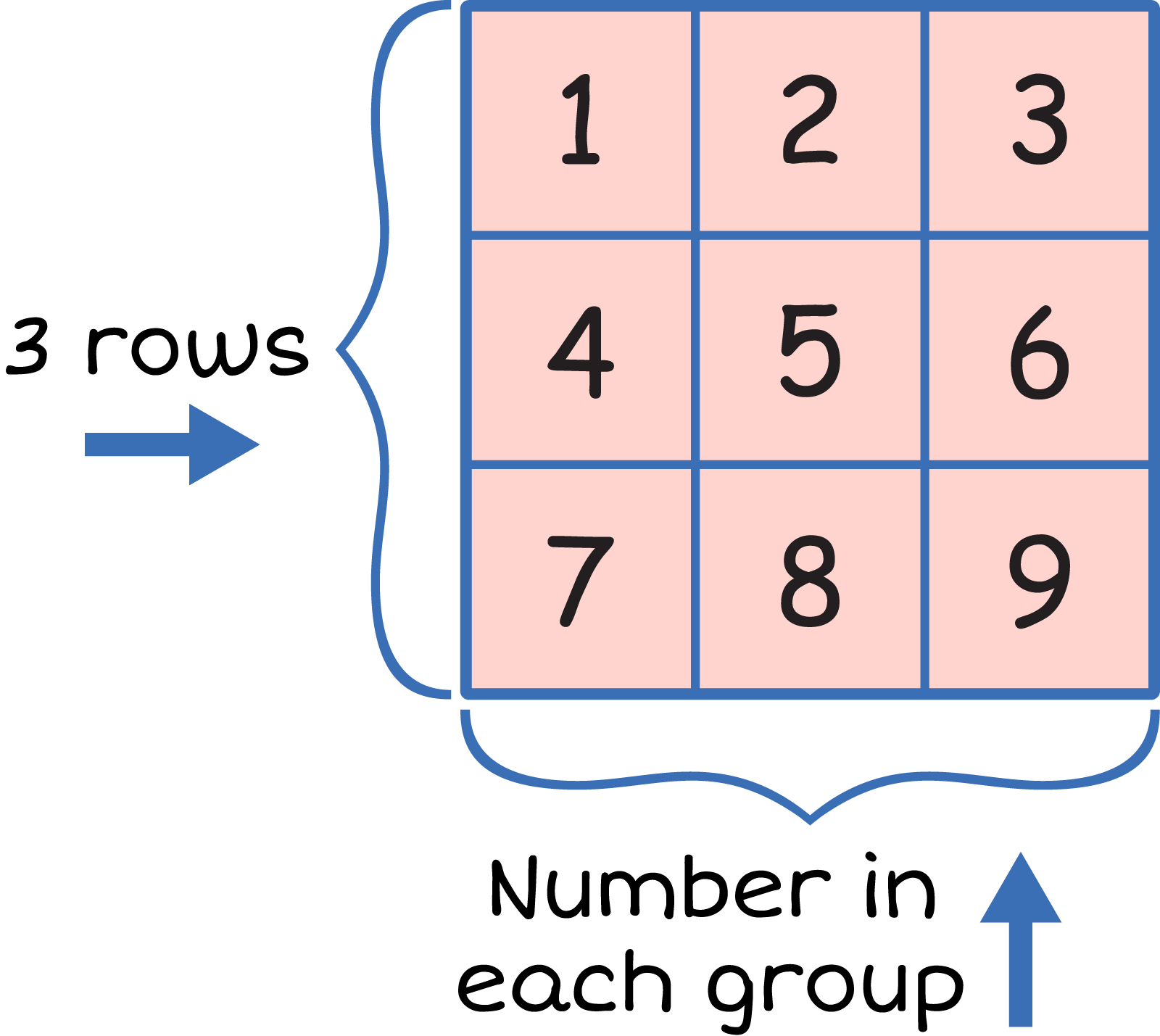 A square tile. Width: 3 Units, Length: 3 Units. Units
are labelled 1,2,3,4,5,6,7,8,9. 3 rows, the units left
to right are the numbers in each group.
A square tile. Width: 3 Units, Length: 3 Units. Units
are labelled 1,2,3,4,5,6,7,8,9. 3 rows, the units left
to right are the numbers in each group.
To write the math sentence, add the number of tiles in each row and the number of rows. Look at the example. There are 3 rows and 3 tiles in each row. So, \({3 + 3 + 3 = 9}\). The area of this rectangle is 9 square units.
What is another way to show 9 square units?
Click the Show Me button to check!
9 units\({\Large^2}\)
Multiplication is similar to repeated addition. You are multiplying the length of an object by its width. The length is how long the shape is. The width is how wide the shape is.
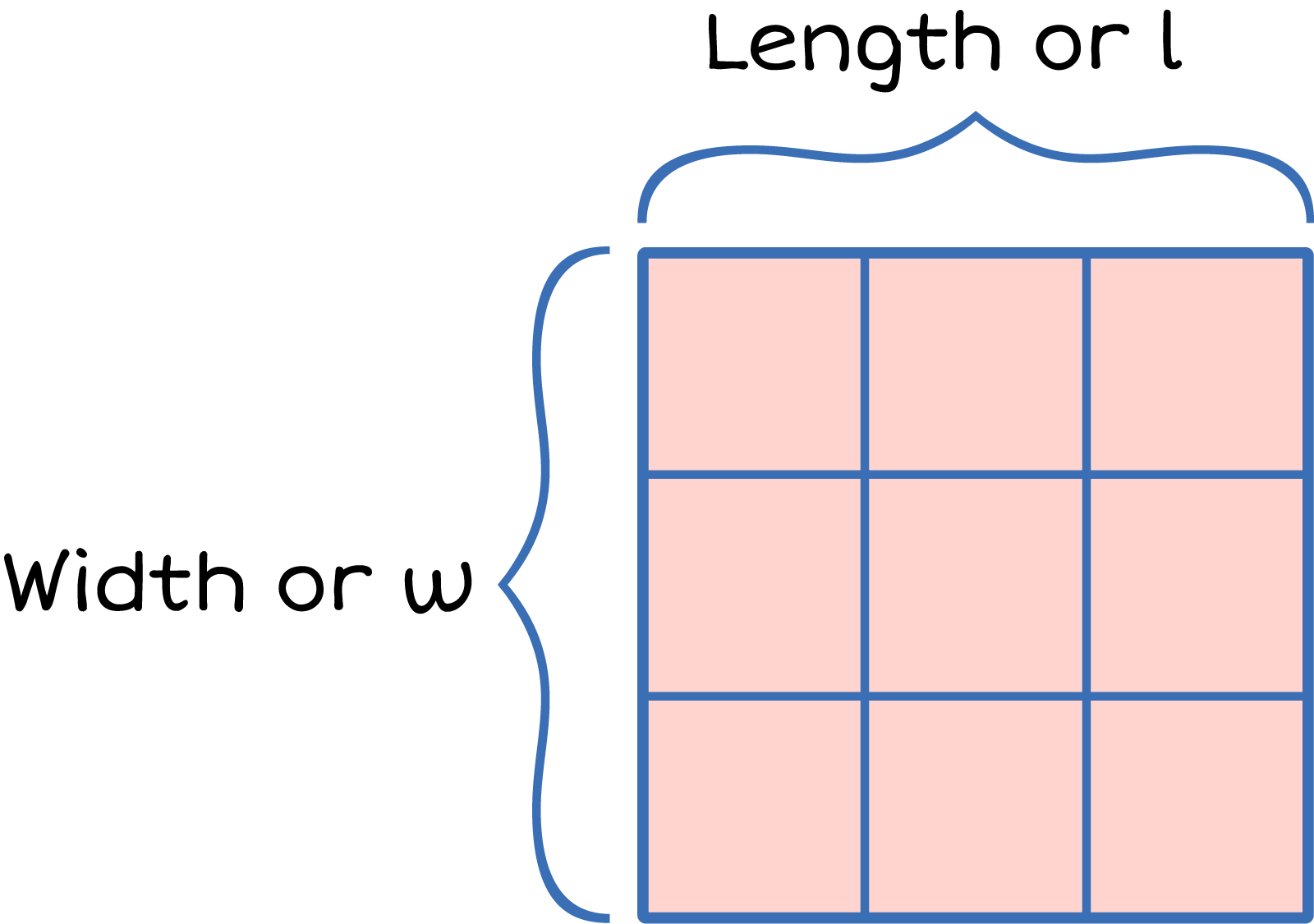 A square tile. Width: 3 Units, Length: 3 Units. The
width is labelled on the left and length is labelled on
the top.
A square tile. Width: 3 Units, Length: 3 Units. The
width is labelled on the left and length is labelled on
the top.
In other words, \({\Large\text{Area} = \text{length} \times \text{width}}\) or \({\Large\text{A} = l \times w}\)
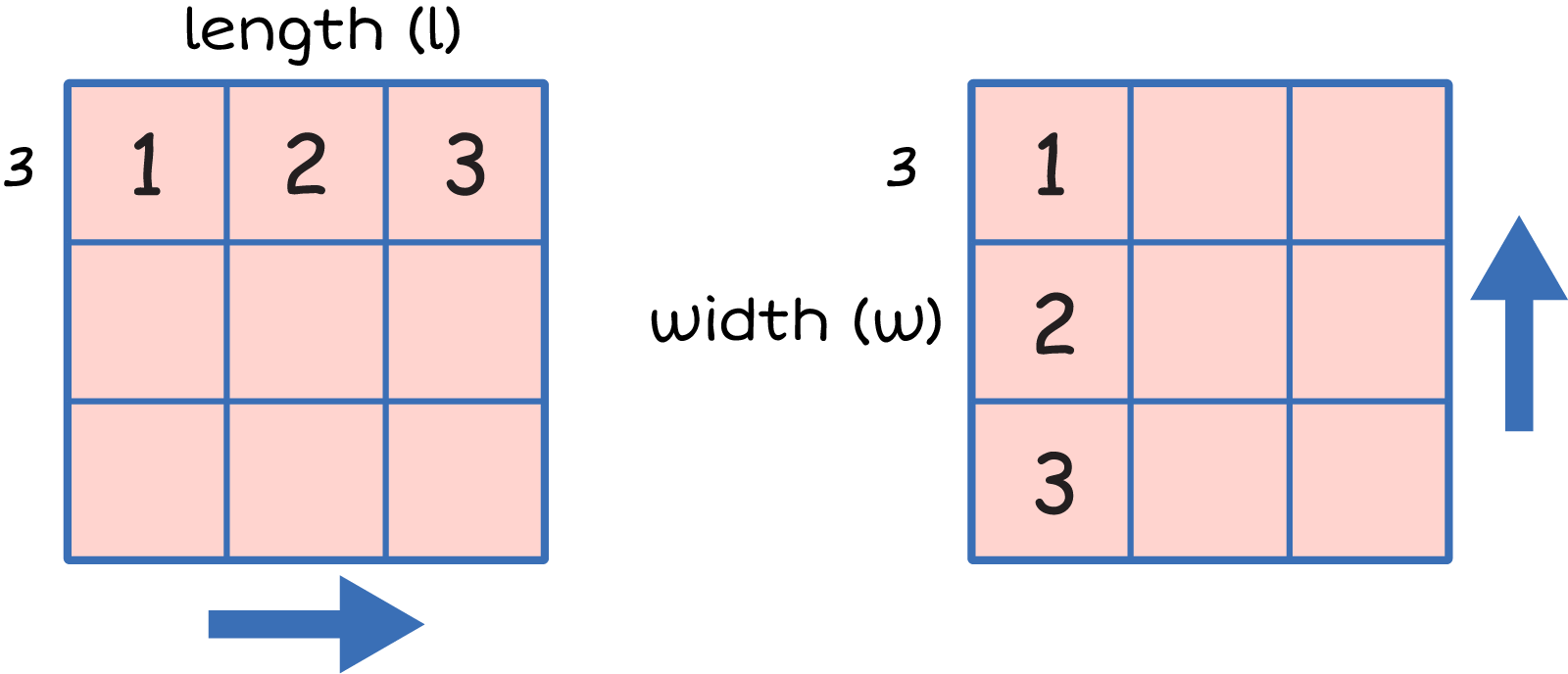 A square tile. Width: 3 Units, Length: 3 Units. The
length is labelled on top. You can count the length by
counting from left to right. In the example it counts
the units in the first row. 1,2,3. The width is labelled
and an arrow shows to count the width from top to
bottom. It counts from the top of the first column down
1,2,3. the top.
A square tile. Width: 3 Units, Length: 3 Units. The
length is labelled on top. You can count the length by
counting from left to right. In the example it counts
the units in the first row. 1,2,3. The width is labelled
and an arrow shows to count the width from top to
bottom. It counts from the top of the first column down
1,2,3. the top.
If \({\Large\text{Area} = l \times w}\),
then
\({\Large\text{Area} = 3\; \text{units} \times 3\; \text{units} = 9\;\text{square units} }\).
Think of it as 3 rows with 3 tiles in each row.
No matter which strategy you use for finding the area--counting, repeated addition, or multiplication--the area is the same, 9 square units!